CCF20091117019

71

GRANICE FUNKCJI - DEFINICJE

Niech funkcja f będzie określona w przedziale (a\xo), gdzie a < xo. Liczba g jest granicą lewostronną funkcji f w punkcie xo, czyli lim f(x) = g, jeśli dla każdego

X-X_Q

ciągu argumentów (x„) zbieżnego do xo o wy razach mniejszych od xo odpowiadający mu ciąg wartości funkcji (f(x„)) jest zbieżny do g.

Niech funkcja f będzie określona w przedziale (x₀;n), gdzie a > xo. Liczba g jest

granicą prawostronną funkcji f w punkcie x₀, czyli lim f(x) = g, jeśli dla każdego

*-^xo

ciągu argumentów- (x„) zbieżnego do xo o wyrazach większych od xo odpowiadający mu ciąg wartości funkcji (f(x_n)) jest zbieżny do g.

.Analogicznie określa się granice jednostronne niewłaściwe. Podobnie jak poprzednio, wystarczy w⁷ powyższych definicjach zastąpić liczbę g symbolem +oo (lub -co), a zbieżność ciągu wartości zastąpić rozbieżnością do +oo (lub do -<»).

Związek między granicami jednostronnymi a granicą funkcji opisują twierdzenia:

Jeśli istnieje granica funkcji f w punkcie xo, to istnieją też granice lewostronna i prawostronna tej funkcji w punkcie xo i wszystkie te trzy granice są równe.

Jeśli istnieją granice lewostronna i prawostronna funkcji f w punkcie xo i granice te są sobie równe, to istnieje też granica funkcji f w tym punkcie i jest ona równa granicom jednostronnym.

Jeśli literą g oznaczylibyśmy granicę funkcji, właściwą bądź niewłaściwą, to obie te implikacje moglibyśmy zapisać w skrócie w⁷ następujący sposób:

lim f (x) = g wtedy i tylko wtedy, gdy lim_ f (x) = lim f (x) = g

X~XQ    x—x₀    ^x~^xo

Podane w⁷ tym rozdziale definicje granic funkcji sformułował niemiecki matematyk Eduard Heine (1821-1881) (czyt. hajne). Przedtem inne definicje podał francuski matematyk Augustin Cauchy (1789-1857) (czyt. koszi).

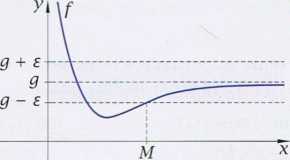
Definicja Cauchy’ego granicy właściwej funkcji w +oo jest następująca:

Mówimy, że liczba g jest granicą funkcji f w⁷ +oo, gdy dla każdego s > O istnieje taka liczba M, że jeśli x > M, to wartość f(x) różni się od g o mniej niż e (czyli jeśli x > M, to \f(x) -g\ < e).

Można udowodnić, że definicje Heinego i Cauchy’ego są równoważne.

J