CCF20091117018

70

GRANICE FUNKCJI. POCHODNE

Podobnie za pomocą ciągów możemy określić granicę dowolnej funkcji w punkcie xo■ Punkt ten może, ale nie musi należeć do dziedziny funkcji.

Aby móc wybierać ciągi zbieżne do punktu xo, musimy tylko mieć pewmość, że funkcja jest określona dla argumentów leżących dowolnie blisko tego punktu. Jeśli z przedziału zawierającego punkt xo usuniemy ten punkt, to otrzymamy zbiór liczb (a;xo)u(x₀;fc), gdzie a < xo < b, spełniający ten warunek. Tak otrzymany zbiór nazywany jest sąsiedztwem punktu x₀.

Teraz możemy już podać definicję granicy funkcji w punkcie:

Niech funkcja f będzie określona w pewnym sąsiedztwie punktu xo. Liczba g jest granicą funkcji f w punkcie xo, czyli lim f(x) = g, jeśli dla każdego ciągu argu-

X—Xo

mentów^? (x„) zbieżnego do x₀, o wyrazach różnych od xo, odpowiadający mu ciąg wartości funkcji (f(x„)) jest zbieżny do g.

Aby sformułować definicję granicy niewłaściwej funkcji w punkcie, wystarczy w podanej definicji zastąpić liczbę g symbolem +co (lub -oo), a zbieżność ciągu wartości zastąpić rozbieżnością do +oo (lub do -oo).

GRANICE JEDNOSTRONNE

f

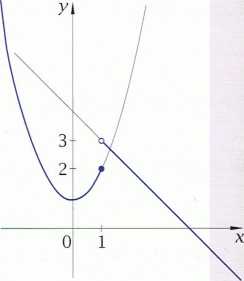
Rozważmy teraz funkcję:

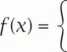
x² + 1 dla x < 1 -x + 4 dla x > 1

Z wykresu widać, że w punkcie 1 granica funkcji f nie istnieje. Funkcja ta ma jednak w punkcie 1 granicę lewostronną oraz prawostronną.

lim f(x) = lim (x² + 1) = 2 lim f(x) = lim (-x + 4) = 3

Za pomocą ciągów moglibyśmy to opisać w następujący sposób. Jeśli wybralibyśmy dowolny ciąg argumentów (x„) zbieżny do 1, o wyrazach mniejszych od 1, to ciąg (f(x_n)) byłby zawsze zbieżny do 2. Z kolei dla dowolnego ciągu (x„) zbieżnego do 1, o wyrazach większych od 1, ciąg (f(x_n)) jest zbieżny do 3.

W podobny sposób definiujemy granice jednostronne dowolnej funkcji.