CCF20091117012

62

GRANICE FUNKCJI. POCHODNE

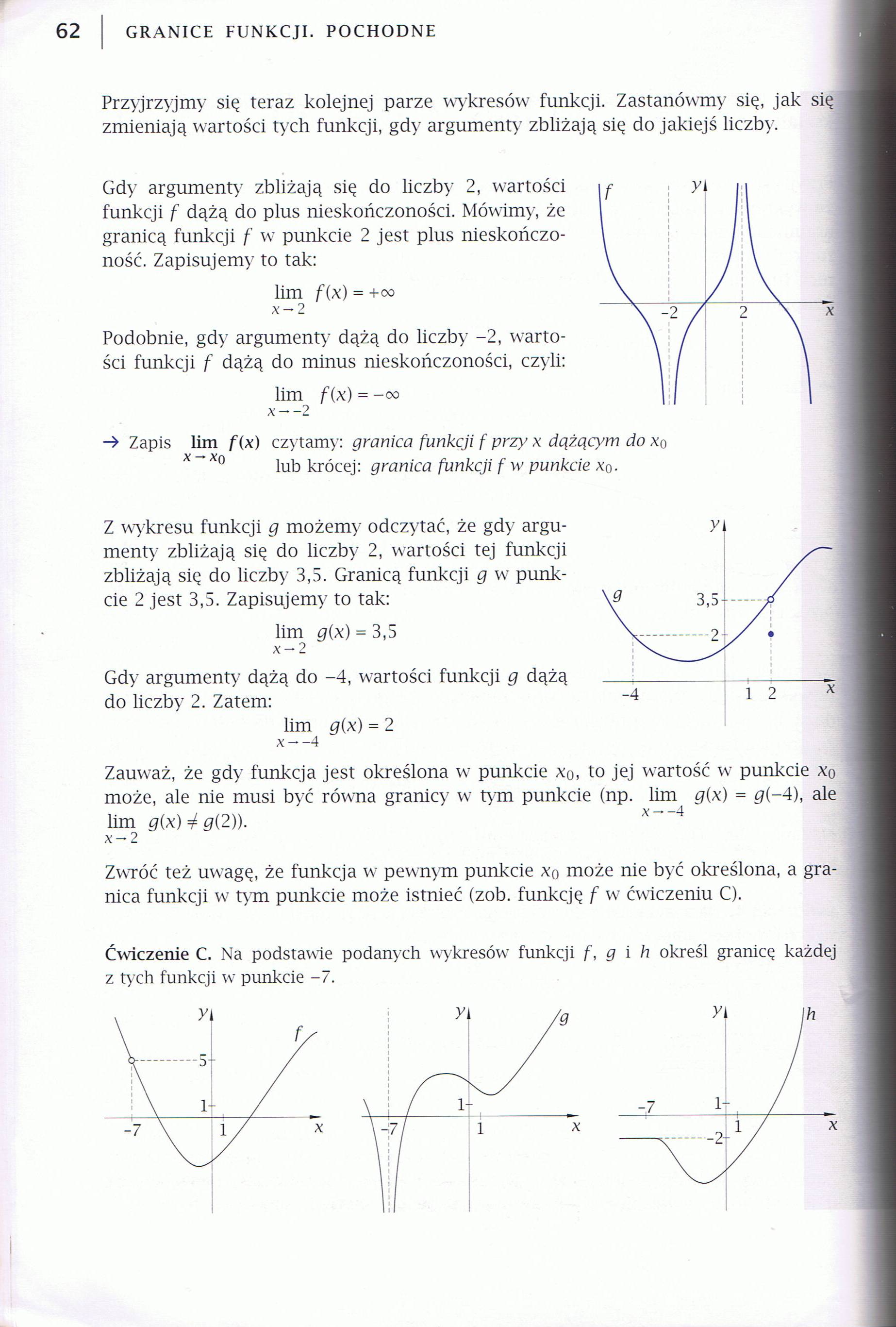
Przyjrzyjmy się teraz kolejnej parze wykresów funkcji. Zastanówmy się, jak się zmieniają wartości tych funkcji, gdy argumenty zbliżają się do jakiejś liczby.

Gdy argumenty^ zbliżają się do liczby 2, wartości funkcji f dążą do plus nieskończoności. Mówimy, że granicą funkcji f w punkcie 2 jest plus nieskończoność. Zapisujemy to tak:

lim f{x) = +oo

x —2

Podobnie, gdy argumenty dążą do liczby -2, wartości funkcji f dążą do minus nieskończoności, czyli:

lim f(x) = -oo

x--2

-4 Zapis lim f (x) czytamy: granica funkcji f przy x dążącym do Xo

x-x₀

lub krócej: granica funkcji f w punkcie xq.

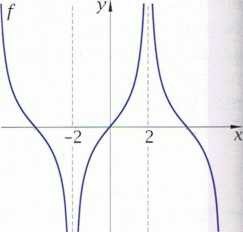
Z wykresu funkcji g możemy odczytać, że gdy argumenty zbliżają się do liczby 2, wartości tej funkcji zbliżają się do liczby 3,5. Granicą funkcji g w punkcie 2 jest 3,5. Zapisujemy to tak:

lim g{x) = 3,5

x —2

Gdy argumenty dążą do -4, wartości funkcji g dążą do liczby 2. Zatem:

lim g(x) = 2 x--4

y i

Zauważ, że gdy funkcja jest określona w punkcie xo, to jej wnrtość w punkcie xo może, ale nie musi być równa granicy w tym punkcie (np. lim g(x) = g(-4), ale lim g(x)4g{2)).    *““⁴

x —2

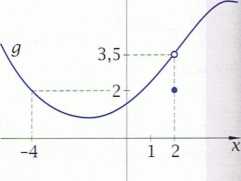
Zwróć też uwagę, że funkcja w pewnym punkcie x₀ może nie być określona, a granica funkcji w tym punkcie może istnieć (zob. funkcję f w ćwiczeniu C).

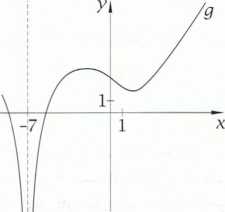
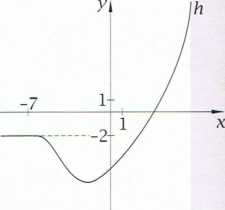
Ćwiczenie C. Na podstawie podanych wykresów funkcji f,g\h określ granicę każdej z tych funkcji w^r punkcie -7.