CCF20091117010

60

GRANICE FUNKCJI. POCHODNE

Granice funkcji - intuicje

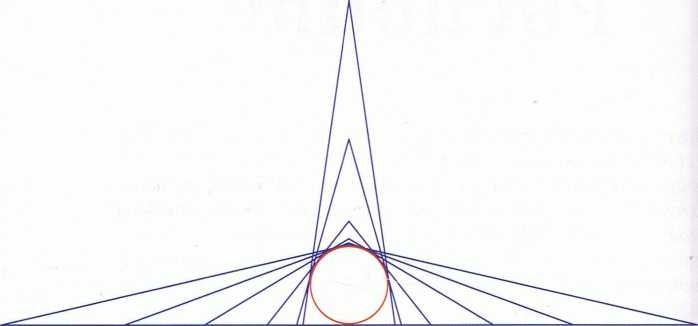
Rozważmy następującą sytuację. Na okręgu o promieniu 1 opisujemy trójkąty równoramienne. Zauważ, że gdy zwiększa się długość podstawy trójkąta, zmniejsza się wysokość trójkąta i zmienia się także długość jego ramion.

Oznaczmy przez x długość podstawy trójkąta. Niech h(x) oznacza długość wysokości opuszczonej na podstawę i niech Z(x) oznacza długość ramienia tego trójkąta. Wyobraźmy sobie, że zwiększamy długości podstaw trójkątów- w sposób nieograniczony. Wówczas wartość h(x) jest coraz bliższa średnicy okręgu, a wartość Z(x) rośnie w sposób nieograniczony.

Możemy powiedzieć, że gdy x dąży do plus nieskończoności, wartości h(x) dążą do 2, a wartości I(x) dążą do plus nieskończoności. Mówimy wtedy, że liczba 2 jest granicą funkcji h(x), gdy x dąży do plus nieskończoności, oraz że plus nieskończoność jest granicą funkcji Z(x), gdy x dąży do plus nieskończoności.

Ćwiczenie A. Zauważ, że podstawa trójkąta równoramiennego opisanego na okręgu o promieniu 1 jest zawsze większa od 2. Jak myślisz, jaka jest granica funkcji h(x), a jaka funkcji Z(x), gdy x dąży do 2?

Z pojęciem granicy spotkałeś się w klasie drugiej przy okazji omawiania ciągów. O granicach możemy mówić także w⁷ wypadku innych funkcji. Zanim jednak pojawią się ścisłe definicje, spróbujemy intuicyjnie przybliżyć to pojęcie.