CCF20091117011

GRANICE FUNKCJI - INTUICJE

61

tym rozdziale będziemy analizować wykresy różnych funkcji. Przyjmujemy, że t wykresu poza narysowaną częścią nie ulega istotnymi zmianom.

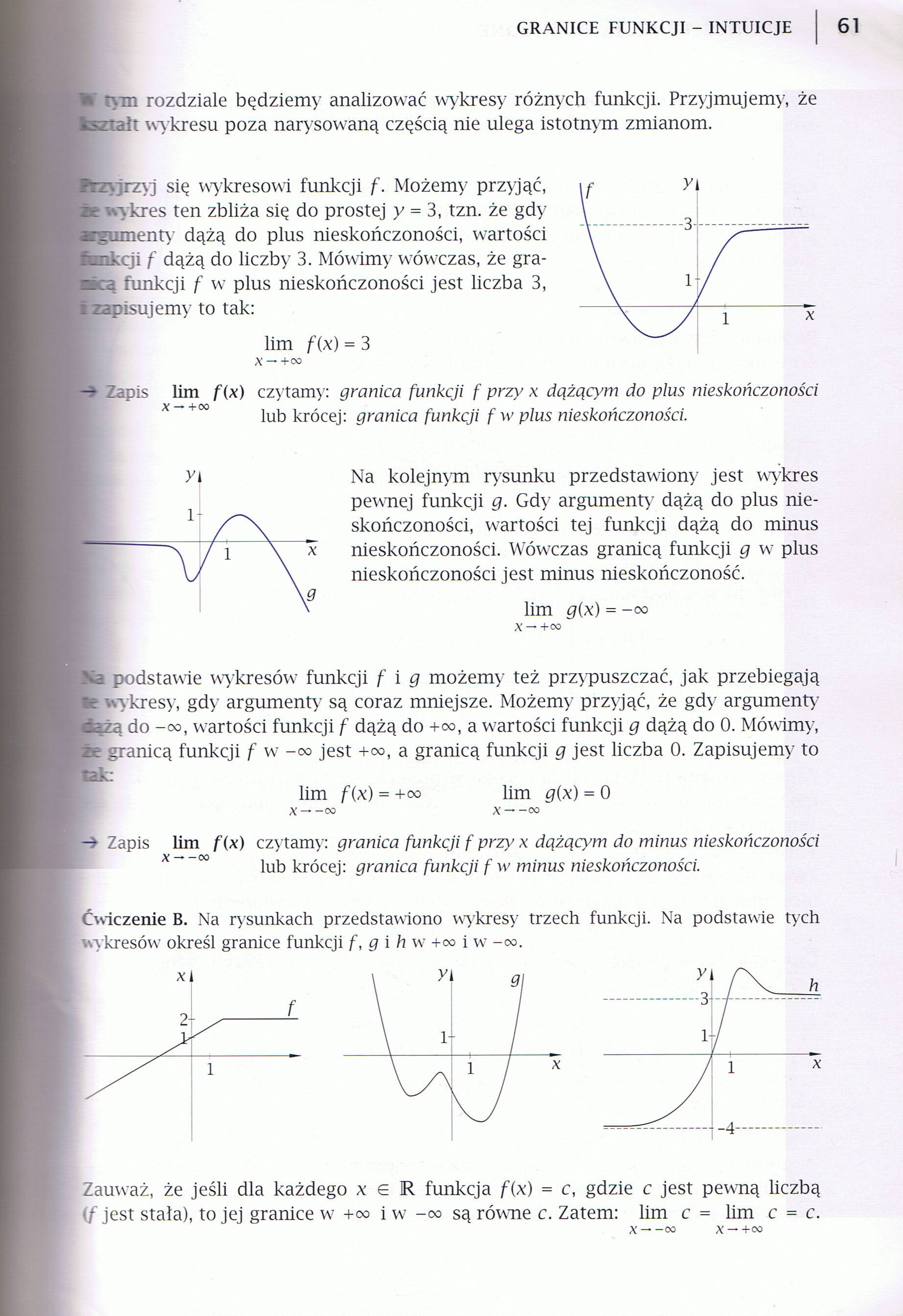
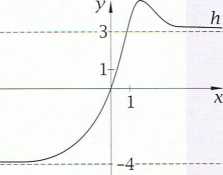
yj się wykresowi funkcji f. Możemy przyjąć, rykres ten zbliża się do prostej y = 3, tzn. że gdy nenty dążą do plus nieskończoności, wartości Iccji f dążą do liczby 3. Mówimy wńwuzas, że gra-funkcji f w' plus nieskończoności jest liczba 3, [zapisujemy to tak:

- Zapis

lim f(x)

X — +00

lim f(x) = 3

X — +°o

czytamy: granica funkcji f przy x dążącym do plus nieskończoności lub krócej: granica funkcji f w plus nieskończoności.

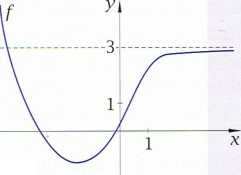
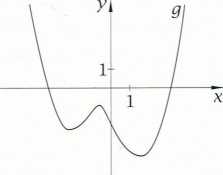
Na kolejnym rysunku przedstawiony jest wykres pewnej funkcji g. Gdy argumenty dążą do plus nieskończoności, wmrtości tej funkcji dążą do minus nieskończoności. Wówczas granicą funkcji g w plus nieskończoności jest minus nieskończoność.

lim g(x) = -oo

X — +oo

podstawie wykresów funkcji f i g możemy też przypuszczać, jak przebiegają Ke wykresy, gdy argumenty' są coraz mniejsze. Możemy przyjąć, że gdy argumenty' dążą do -oo, wartości funkcji f dążą do +co, a wartości funkcji g dążą do 0. Mówimy, 1 że granicą funkcji f w -co jest +oo, a granicą funkcji g jest liczba 0. Zapisujemy to

lim f(x) = +oo    lim g(x) = O

X--00    X--00

—> Zapis lim f(x) czytamy: granica funkcji f przy x dążącym do minus nieskończoności lub krócej: granica funkcji f w minus nieskończoności.

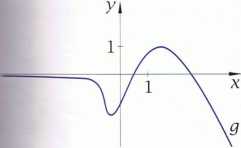
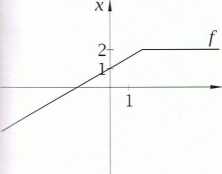
Ćwiczenie B. Na rysunkach przedstawiono wykresy trzech funkcji. Na podstawie tych wykresów' określ granice funkcji f,gihw +oo i w -oo.

Zauważ, że jeśli dla każdego x e R funkcja f(x) = c, gdzie c jest pewmą liczbą (f jest stała), to jej granice w +oo i w -oo są równe c. Zatem: lim c = lim c = c.

X —* —co    X — +co