CCF20091117020

GRANICE FUNKCJI. POCHODNE

zadania

i.

a)

b)

Korzystając z definicji granicy, oblicz: lim ^{2x + 1}

X — +oo

X-

6x-

c)

lim — , „

Y —* 4-00 7 + 10X

lim

X--00

2x - 5 7-3x

d)

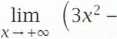
2

x

)

2.    Korzystając z definicji granicy funkcji w punkcie, oblicz:

a) lim (2x-3)    c) lim (ix² - 2)

b) lim (—ix + 4)    d) lim —

3.    Korzystając z definicji granicy, wykaż, że nie istnieje granica funkcji:

a)    f (x) = i w punkcie O,

b)    f (x) = cos x w minus nieskończoności,

c)    f(x) = tgx w punkcie y.

® 4. Wykaż, że funkcja okresowa, która nie jest funkcją stałą, nie ma granicy w plus nieskończoności i w minus nieskończoności.

® 5. Funkcja f, zwana funkcją Dirichleta, określona jest w następujący sposób:

f 1 dla x wymiernych (_ O dla x niewymiernych

Wykaż, że funkcja ta nie ma granicy w żadnym punkcie.

Funkcje ciągłe

Ćwiczenie A. Narysuj wykres jakiejkolwiek funkcji f, której dziedziną jest zbiór liczb rzeczywistych i która spełnia warunek:

a) lim f(x) = f( 1)    b) lim f(x)4f( 1)    c) liny f(x) = 1 i lim f(x) = 3

x—1    x—1    x—1    x—1⁺

Zauważyłeś już zapewne, że często granica funkcji w danym punkcie jest równa wartości funkcji w tymi punkcie. Jednak nie zawsze musi tak być.