2567802552

Niech funkcja /: / x R —* R będzie określona wzorem:

oraz

t = 0.

l 0, t = 0.

Rozważmy następujące zagadnienie Cauchy’ego:

f*'(0 = /(t.*(0),

1    x(0) = 0.

Rozwiązaniem wyżej wymienionego problemu jest funkcja

f_gt³/3j^_e ^s3/³F'(s)ds, t 0

l 0,    t = 0,

0,

t = 0,

gdzie F(t) = t² sin t~².

Zauważmy, że funkcja F'(t) nie jest funkcją całkowalną w sensie Lebesgue’a. Stąd znaleziona funkcja x(t) nie jest rozwiązaniem rozpatrywanego zagadnienia Cauchy’ego przy założeniu całkowalności funkcji f w sensie Lebesgue’a. Pojawia się więc konieczność rozszerzenia klasy całek.

W części swoich badań wykorzystuję uogólnioną postać całki Henstocka-Kurzweila z funkcji o wartościach w przestrzeniach Banacha w celu uzyskania twierdzeń egzystencjalnych, dotyczących nieliniowych równań całkowych, różniczkowo-całkowych i różniczkowych, w tym także równań rzędu m oraz równań z odchylonym argumentem.

Ze względu na fakt, iż całka Henstocka-Kurzweila jest uogólnieniem wcześniej znanych całek, np. całki Bochnera, wyniki przedstawiane przeze mnie, uzyskane zostały dla szerszej klasy funkcji niż dotychczas znane.

Rozpatrzmy teraz następujący przykład (omówiony w pracy (6)).

Niech E oznacza przestrzeń Banacha, F* - przestrzeń dualną do przestrzeni Banacha.

Niech /: [0,1] -» (L°°[0,1], IHIco) oraz /(t) = j[o,t] + A(t) ■ F'(t), gdzie F(t) = t² sin t ², te(0,l],

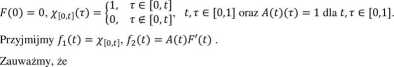
Ponieważ funkcja    jest całkowalna w sensie Lebesgue’a, więc funkcja jest całkowalna w

sensie Pettisa. Funkcja x*(f₂(ty) jest natomiast całkowalna w sensie Henstocka-Kurzweila. Ponieważ dla żadnego x*eE*, funkcja x*f nie jest całkowalna w sensie Lebesgue’a, więc funkcja / nie jest całkowalna w sensie Pettisa. Ponadto, funkcja f_t nie jest silnie mierzalną funkcją, a f₂ jest silnie mierzalna. Zatem funkcja / =    + /₂ nie jest silnie mierzalna i na mocy twierdzenia 9 [33] nie jest

całkowalna w sensie Henstocka-Kurzweila.

5