30267 MATEMATYKA117

mm

224

IV Całka nieoznaczona

4. CAŁKOWANIE PEWNYCH FUNKCJI NIEWYMIERNYCH

CAŁKI TYPU jR(x*^“^j)dx* gdzie litera R oznacza tutaj

(i w całym paragrafie) funkcję wymierną swoich argumentów.

Każdą całkę tej postaci można sprowadzić do całki funkcji wymiernej zmiennej t stosując podstawienie

i

ax+b

cx+d

= t.

Szczególnym przypadkiem rozważanej całki jest całka J R(x_? Vax+b )dx. PRZYKŁAD 4.1 Obliczymy całki:

= ^t⁵-14t+C=~Vx + 4(x 17) ₊ c

. r ^dx _ f (Vx )³dx    x*i⁶l f    .

^b J x^x(Vx -4) "J x'Vxi(>/x)²-4) \ dx=6t^sdt j J t⁷(t² -4) ~

=3j-^-dt=3ln|t²-4|+C=31n|Vx ₄|,_C

r d\    r    dx    _fVx^T»i. x-i+i⁴

^c)J^_x:i^T^^SJ^-i<(Vx-i)²+4)"l <łx■ 4i\it

₌ fji^ = 4f4^ = 4f(ł-_T^_r)dt-4t--Harctg-l _{+ r}

Jt(l^J+4) Jt²-f4 J l*+4    ⁶2^4C =

- 4 Vx-7 - Kardg-^^l ₊ ^

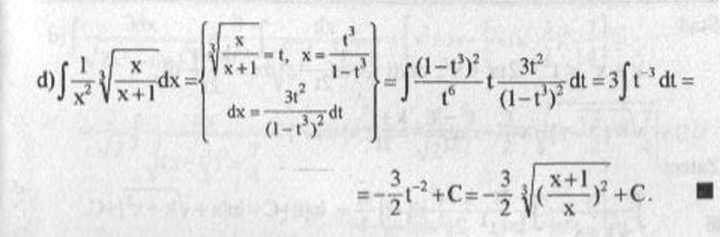
CAŁKI A BELA. Są lo całki postaci

J R(x,Va>? + bx + c)dx.

Każdą całkę tej postaci można sprowadzić do całki funkcji wymiernej zmiennej l stosując jedno z tzw. podstawień Eulera:

Jsl\² + bx+c = t±xVa, gdy a>0,

Vax² + bx+c = i\±Jc, gdy c>0,

>/ax² + bx+c = t(x-a), gdy Ar-b²-4ac>0, aa jest jednym z dwóch pierwiastków równania ax² + bx+c = 0.

Podstawienia tc wymagają jednak długich rachunków. Dlatego postąpimy inaczej - wyróżnimy najpierw kilka takich całek, obliczymy je, a następnie inne trudniejsze, będziemy sprowadzać do tych wyróżnionych.

A. Najprostsze całki Abela, lo a) f -71——. b)

^Jyk--x² J vk+x²

a) Pierwszą z nich, stosując podstawienie x = Vkt, wyznaczyliśmy w przykładzie 2.3 c:

(4.1)    -=arcsin-i+C, k>0.

^J7T7 Vk

b) Aby obliczyć drugą z tych całek, zastosujemy pierwsze podstawienie Eulera:

Vk+x² =t-x.