35036 MATEMATYKA111

212

IV. Całka nieoznaczona

2. Metody całkowania

213

O d p o w i c d z i ( podane są / dokładnością do stałej całkowania).

*• tt)^x^,-yx^z + x, b) x~arctgx, c>2tgx + x, d)~jr,x>0,

2. n) jy(x² + l)¹, b)-jcon³x, c) ~<x^J + l)Vx* + l. d) yc^T, c)~ e~*\ I) 2c^*. ⁸⁾1ńx* ^h)^_2^,n'¹“^x21, »)jon;tKX², j) ~(Hrvtgx)*, k) nrctge*. l)-j(x+l)-^J+i(x + l>\ l)|(x-l)U|<x-l)5.    n) tg(lnx),

o) -sin(l-c*), p) —ln|3—lnx|, q) -^arctg^~, r)-^-arctg-^,

s) -^>arctg(V2c^x), t) ln|sinlnxf, u) yarcsin2x, v) arcsin^-, w) ^-arcsin^^-, x) ■^•cosh^ńx, y) jsinhxV-siuhx, z) sinhx(l+ysinh²x+ysinh⁴x), wsk. wykorzystać równość cosli² x-sinh² x = 1.

3.    a)-2lnⁱx³-x+2|, b)-jln|3-5x|, c)ln(l+sin²x), d) łn|smx|, e)-ln(arccosx),

Oln{e^x+l), g) ln(4+coshx), h) 2arc1gx-2ln(l + x²), i)lnftgy|.

4.    a)2t/2x²-x+l, b)    , c) 2>l\+<f , d)-Vl+cos²x ,

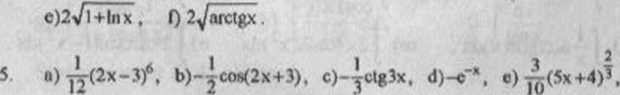
0^arcRin3x, g) ^-n/ctgxV5, h) ~$inh(2x+3).

i) ~(sin2x-cos2x)e^2x, j) ~(-sin2x-2cos2x)ek) xlgx+ln|cosx|,

I) *y-xcig3x+^łnjsii\3x|, ł) -Vl-x²urccosx-x_l in) xln(x+Vx²7k)-‘>[xF+k ,

7    a)|-x^(ln²x-3lnx+~),b)x(ln²x-2lnx+2),c)x(arcsinx)²+2Vl-x² arcsinx-2x,

d) yX(sinlnx-COslnx)_> e) ~x²(2coslnx+sinlnx), ł) y(x³ + IXln(x³ + l)-l), g)y(x²-l)e^x\ h) -y-(x³-*-l)c ^-x\ i) (ln²(lnx)-2ln(lnx)+2)łnx ,* j) 2(l~cosx)c^c,n\ k) (tgX‘-l)c^,ff', 1) (lnarctgx-l)arctgx, ł) lnxarctglnx-^ln(l + ln²X)_ł m) x²sinh(x²)-eoih(X²),

n) (x²-l)arcsin(l-x²)-V2k³-x⁴.

8.    a) J_n = -^sin^ft_lxcosx+~^;_n_₂, n=2,3,..,,

...    1 sinx n-2»

^{} n =} ^^rt⁺^^^2,n=2,3.....

c) J_n = xln"x-nJ_n_,, n = lji.....

9. a)-^8sirr⁵xcosx+10sin*>łco8X+15sinxcofX’-15x),

h).    ■■+~tgx, c)x(fh³x-3ln²x+6lnx-$).

3cos^Jx 3

1

a)-“Xcos2x+^-sin2x, b)-yx²cxw2x+yXsin2x+^-cos2x.

c)~(x^}+3x^z+6x+6)c“^x> d)~X³(31ii2x— 1). e)xln2x-x,

I    o    i    r—

0 Xarclg2x-^ln(l+4x²), g) j(x²arctgx+arctgx-x). h) xarcsinx+V l-x² ,