MATEMATYKA106

202 IV. Całka nieoznaczona

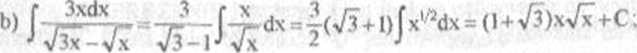
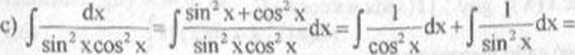
= tgx-ctgx+C

Całkowanie przez podstawienie

TWIERDZENIE 2.1 Jeżeli;

1)    funkcja g(t) jest ciągła na przedziale <a,p>,

2)    funkcja l = h(x) jest klasy C¹ na przedziale <a,b>.

3)    funkcja h odwzorowuje przedział <a,b> na przedział <a,p>,

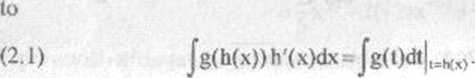
(Zapis po prawej stronic oznacza, że po obliczeniu całki g(t)dt zmienną

t należy zastąpić przez h(x), czyli jak mówimy, "wrócić do starej zmiennej*⁴).

D o w ó d Założenia zapewniają ciągłość a więc i całkowalność funkcji podcałkowych po obu stronach równości (2.1). Pozostaje wykazać tę równość. W tym celu wystarczy wykazać, że pochodna względem X prawej strony (2.1) jest równa funkcji podcałkowej po lewej stronic. Niech więc

Stąd

;(t)dt = G(t) + C, G'(t) = g(t). Jg(t)dt|_l=;h(x) = G(h(x)) + C.

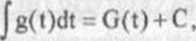
Zatem

f 8(t)dt|, _wG(h(x)) + C) = G'(h(x))h'(x) =

= g(h(x))h'(x).    □

Zauważmy, źc całka po prawej stronic wzoru (2.1) na całkowanie przez podstawienie powstaje z lewej strony przez zastąpienie funkcji h(x) zmienną t i różniczki h'(x)dx różniczką dt zmiennej t. Zatem: aby dokonać zamiany zmiennej w całce nieoznaczonej należy wyrazić przez nową zmienną, zgodnie z j>odstawtentem, całe wyrażenie f>odcałkowe

P R Z Y K ł. A D 2.2 Obliczymy następujące całki nieoznaczone:

a) f2xe«‘dx    _e._+c| _=e^x’₊c

J    [wtedy 2xdx«*dt    j J    x^ł

W następnych przykładach będziemy stosować bard/jej /.wię/Jy i skrócony zapis.

b)    | ^yc^lxdx ⁼ |“ ⁼ t. 4-dx a -dt J — J c*dt = —c* + C= e^l/x + C,

c)    J(\^: fx^l)''(2x + l)dx = {x²+x+t = t, (2x+l)dx = dl}=JVdl = V+C =

₌ ^(_X2 ₊ X+1)⁵+C,

d)    [—~— = jlnx = t, — dx = dll= [4pdt=—--j-C = —— + C

Jxln²x [ x J J r _t Uhc ’

^C^J x(T+in^2_x) ~{^ll,x -^l« -^dx = ^dt|' 2j-p-L-dl = 2arctgt-fC - 2arclg(lnx)+C, 0 f —^>S,—d\-{smx = t, cosxdx = dt} fJj. _.7.1 ,r-    * ,r

^s'^{n x}    V 2t^ł 2sm’x ’

r 3c*dx r v v i p dt

B)JT" ~^-\^c "^l,c <łx-dij=3J-p—= 3arc$int+C=3arcsin(c')+C. v I-c    Wl-t*

r varcs

^h) J 7TT

^nrc»ⁱ"’^<”'.^-_rd_X=dt

= |tV»dl=lt^4C

Varcsin x .

= ^-arestn x Varcsinx +C.    ■

v. , • ^^s^^Łazani® podstawień w tym p_rzykladzic mc sprawiło kłopotu. Niekiedy jest to jednak trudniejsze