MATEMATYKA105

200 IV. Całka nieoznaczona

TWIERDZENIE 1.4 Jeżeli f jest ftmkcją całkowalną na pewnym przedziale, k jest stałą, to funkcja kf jest również całkowalna na tym przedziale i gdy k * 0, to

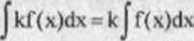
Zauważmy, te dln k*0 równość (1.6) jest fałszywa, bo jej lewa strona jest zbiorem nieskończenie wielu ftinkcji stałych F(x)«C, prawu natomiast przedstawia tylko jedną sialu funkcję F(x)«0

Ostatnie dwa twierdzenia rozszerzają klasę funkcji, które już teraz umiemy całkować.

PRZYKŁAD 1.3

a) Jdx = J(x^ - 2x ^V2)dx=Jx^V2dx-2jx“^wdx=

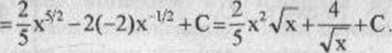
Poprawność otrzymanego wyniku potwierdzimy różniczkowaniem:

Całka została poprawnie obliczona, bo jej pochodna jest równa funkcji podcałkowej.

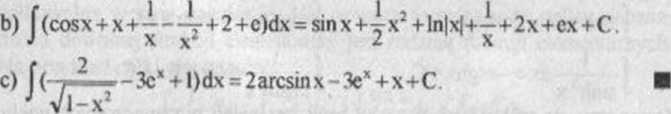
ZADANIA DO ROZWIĄZANIA

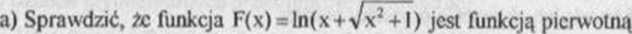
funkcji f(x)= l/Vx² + l na przedziale (-00,00).

b) Czy- funkcja F(x) = —i-arctg(V2ctgx) jest funkcją pierwotną fun-

kcji f(x)=l/(l+cos²x) na przedziale (0,7t)?

c) Znaleźć funkcję pierwotną funkcji f(x) = 2x, która dla x = 0 przyjmuje wartość 1.

2.    Obliczyć: a) (J^_xdx)’, b)J(Vu7)'dx, c) |(cos^:x)'dx

3. Znaleźć f(x), gdy jf(x)dx = xcosx+C.

4.    Obliczyć całki nieoznaczone:

a)J(x4~)dx,

d) J(x-Vx)²dx,

^e) I^<2X-Tn?^)dX’

0j2”dx,

„ra-»ć

b)J(x- l)(x +2)dx

V f xVx-Vx

^C)J" “^dXl

sin* X X^J

—-_r-cosx)dt, cos t

J <un v v

cos' t Odpowiedzi.

1. b) Tak, c)F(x)-x*+l.

j)J(—3— cosl)dt,    k)J (

2. a) l/cosx, b)Vl + x² +C, c) cos² x+C.

3. f(x)=»cosx-xsinx. 4. a) x²/2 + ln|x|+C, b) x³/3+x²/2-2x+C, c) 3>/x^+C, d)xV3-4x²Vx/5+x²/2+C, c)6$?/s~lnx+C, t)2^K/ln2+C, g)x² 3arctgx +C\ h)-2cigx-)/2x²+C, i)2e^x+C, j) tgt-sint+C, k) tgt-tcosx+C,

I) -x^ł/u-3x²ln u|+3xu-u²/2+C.

2. METODY CAŁKOWANIA

Omówimy Irzy metody całkowania całkowanie przez podstawienie, całkowanie przez części i metodę wzorów rckurencyjnych Przed tym zwróćmy jednak uwagę, że często zwykłe algebraiczne przekształcenie funkcji podcałkowej upraszcza całkowanie Ilustruje to

PRZYKŁAD 21

a)    ^ dx = J(ł-2x ¹ +-^)dx = x-4v^x+lnx+C;