21629 MATEMATYKA110

210 IV. Całka nieoznaczona

-A ^d)		c)	j*xc ^X?dx,
g)	f dx J xin^2 x	Vh)	f—^2 dx, * 1 - x^2
j>J		^k)	f dx-f	i) f ..
	' l + x^2		Jc^x+C ^x	^J (X ł 1)

m) pf .

^J sin x ^P) 1 xO-lnx)'

dx

xcos'(lnx)

sinxdx

1) | \yj\~ ld\ . o) jVco$(l-e^x)dx,

_u)j

'!>) J

J|-clg(lnx)d\. W)

^J xV3-41n* x

y) JcoshxVsinhxdx, z)Jcosh-xdx.

3. Stosując wzór (2 3) bliczvć:

^ d) Jctgxdx,    c)J-^ -^dx-

g) J ^smhx

COS* X

X)|

dx

x(3 + ln^: x) dx

V1 - 4x² ’ sinhxcosh⁵\dx

U j ^C‘^dx

V,f

1 + 2c^2x e^xdx

v^4 -c²’

■dx,

^h>I

l-x' arccosx 2 -4x .

4+coshx    J    j _{+ x}2

4. Stosując wzór (2.4) obliczyć:

4- a) f    dx, ^vb) f-X_.dx.

^J V2x²-x + l    ^JVl    + x^ł

d) f smxcos_Łdx, "V e)    f

^JVl+cos‘x    ^J

l + e~* i)

J sinx ^#

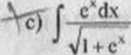
A o f-r-1

^J (l + x*

dx

tyarctgx

5. Stosując wzór (2.5) obliczyć:

^ a)J(2x-3)'dx, b)Jsin(2x +3)dx, c)J-r^dx, d)jV*dx,

6. Slosując twierdzenie o całkowaniu przez części obliczyć:

-+ ^e) f 4.^ '0    g) f , t ₂ , h) fcosl.(2x + 3.)dx

¹ J V5x-4 4 J Ji. 9x^:    Jl + 5x² J

-f a)Jxsin2xdx,	b)|x sin2xdx,	c)JVe ^sd.\,
d)|x^; In2xdx,	. e) |ln 2xdx,	■4- 0 Jarclg2xdx,
g) J xarclgxdx ,	^1 h) J arestn xdx,	i) jV*sin2xdx.
j) jV^xsin2xd\,	k) f V-dx, ^J cos‘X	1) |-4-dx. ^J sin 3x
1) —arccosxdx. m) fln(x + ^J Vl-**		x/x' +k)dx
Obliczyć:
\ f ln^2x . ^a)Jl7r^dx’	b) j In- xdx,	c) j*(arcsinx)^2dx.
d) jsinlnxdx,	e) Jxcoslnxdx,	0jx^2ln(x^> + l)dx>
g)jVe^x‘dx,	h) Jx‘^;e * dx ,	^ j ln^:(lnx)
» j) Jc^eQłXsin2xdx,	k) f ^Si",^X C^dN, ^J COS X	I) r'»(i.rc«!4x)dx J l + X“
1) |4arctg(inx)dx,	m) J 2x^,cosh(x^:)dx,	n) J2xarcsin(l - x)dx

8.    Znaleźć wzory rckurcncyjnc dla całek:

a) J„ = fsinⁿxd.\. b) J_n - f—, c)J_n=flnⁿxdx ^J    J COS X    ^J

9.    Korzystając z wyników zadania 8, obliczyć:

a) f sin⁶ xdx,    b) f—4—,    c) f In' xdx .

j    ^J COS X    ^J