78426 MATEMATYKA118

226 IV. Całka nieoznaczona

226 IV. Całka nieoznaczona

k + x² = t ' - 2tx -ł x\ czyli x =    ^k■, dx = ^k*₂-dt,

r—z , _v_* t²-k kft²

2t k-M²

Sl«|d

Zatem

JkTT²l?^_dl=/f ^ln|l|tC NxWk_+x^J|₊c

Otrzymaliśmy w ten sposób wzór

(4.2)    f «-^d i ~ln(\-f Vk+x“| tC.

^J vk 4-x²

Bezpośrednio z (4.1) i (4.2) mamy na przykład:

^J yj7-x² dx

7+x

J-r^dx==aresin-^+C,    j* ^^=ln(x+y/7 + x² )+C,

f-74^X^=In|x t-Vx²-7|-ł-C, f-i ^dx -= ,-arcsm^+C.

^J vx²-7    ^JV8-2x² V2 2

B Całki postaci

| dx-_

Vax + bx -t c

przekształcając mianownik do postaci kanonicznej i stosując (często "w pamięci") odpowiednie podstawienie, sprowadzamy do całek postaci (4 I) lub (4 2).

PRZYKŁAD 4.2 Obliczymy całki

a)f-. ,m.\    ~^{² *x-x²«-(x²+4x-2)b 1 f dx

^J v2-4x-x^ł l.-((x^,+2)^,-«)-«-<**J)^,J > J<>-(\+2)² ~

{x+2-tl f dj    I    x + 2

dx=dt    »={ uyór(4,l)} = aresin-y-+C=aresin —+C;

hh_r ^TT⁼'    ^{<4 i> 1}" ^^ln|^x~ 5 ⁺i*^x"T^): -1 j^+c=

X-^ + yX²-3.\+y

C Całki postaci

Ax+B

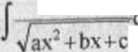
przedstawiamy jako sumę dwóch znanych już nam całek Ax + B . r 2ax+b . „f dx

J-.^{Ax + B} d.x-«f.^2Ł - + 1 ^J yjax²+bx+c    ^Jyax*+bx+c

+bx+c

gdzie 2ax t b = (ax‘ ł bx ♦ c)\ zaś a i p są tak dobranymi współczynnikami, aby

Ax iB * a(2ax+b)+p.

PRZYKŁAD 4.3 Obliczymy całki:

a) (-,±11 dx=a [■■. ~^2x~⁴—dx+P -

^JV2-4x-x-’    ¹ V2-4x-x^:    W2-4x x^!

-2f-₇.:^2x-⁴ dx-5 ^J V2-4x-x^r

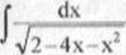
|łx + 3«u(-2x-4)+(i ~\ a--2. (U-S

*{ wzór(2.4) i przykład4 2 a)} = -4^2- 4x-x‘ -5arcsin    +C;

Vr>

b)f-j—S-dx=a [-7 ².^x~.² -dx+p (-_!-dx =

^JVx²-2x-7    ^JVx²-2x-7    ^JVx²-2x-7