MATEMATYKA112

214 IV, Całka nieoznaczona

3. CAŁKOWANIE FUNKCJI WYMIERNYCH

Całkowanie ułamków prostych Przypomnijmy (por. rozdział I), żc funkcją wymierną nazywa się iloraz dwóch wielomianów. Każdą funkcję wymierną można przedstawić w postaci sumy wielomianu (być może równego zeru) oraz ułamków prostych pierwszego i drugiego typu, tj. funkcji wymiernych właściwy cli odpowiednio postaci:

gdzie A = p²-4q <0.

A _ Ax + B (x-a)^nt (x"² + px + q)ⁿ ’

Całkowanie funkcji wymiernych sprowadza się więc do całkowania wielomianów i całkowania ułamków prostych.

Całkowanie ułamków prostych pierwszego typu jest prostym ćwiczeniem na całkowanie przez podstawienie albo wykorzystanie wzorów (2.3) łub (2.5). Ilustruje to

PRZYKŁAD 3.1

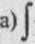
2 dx 3x - 4

3x-4 = t dx = jdt

⁼ łJt ⁼ ł^,n|l|+C=f^,n|3x'^4|fC

albo inaczej:

lś^4^{d,i =} fjl^4^<,’^<= <    > = |ln(3x-4|+C;

^b>!

2dx

(3x-4)⁵

3x-4»t

dx»-jdt

fjr⁵di.f(-lr⁴)₊c

6(3x-4)⁴

+ C

albo na podstawce wzoru (2.5):

J^“²f^(3x-^4r’^dx ^{= 2}T>’‘-⁴>'^,+c

>1

+c.

(3x~4)> ^J' ’    -^ł "⁴    '    6(3x-4)⁴

Całkowanie ułamków' prostych drugiego typu jest trudniejsze.

Rozpatrzymy kolejno przypadki szczególne A. Jeśli k>0,to

f—-

k + x²

x - Jk t dx » Adi

r Adt ₌j_ Jk + kt² Vk

arctgt +• C - -i»arctg-*Ł- + C.

Zatem, jeśli k>() (wtedy A<0), to

(3.1)

f dx 1 •*k+x² A

arclg-W + C.

7k ^g7iT

PRZYKŁAD 3.2 Obliczymy całki: dx

dx    f dx    fx»At )    p Ądl _ 1 f dl

J-3-x²    J 3+x² [dx-V5dtJ    J 3-#-3t²    ^J|+|²

= -^arclg_t+C---L_arctg-|₊C. Oczywiście wynik ten możemy uzyskać stosując bezpośrednio wzór (3.1).

^b)J-y⁵— “ f f“TT “ {^wzór <^{3 1}) }= ^-arcig-⁵^+C.    ■

^J3x^z+4 ^3JX*+⁴    6    2

B Całki postaci

[ dx

Jx²+m

gdzie A = p² - 4<| < 0,

px+q

przekształcając mianownik do postaci kanonicznej, sprowadzamy do całki postaci (3.1).

PRZYKŁAD 3.3 Obliczymy całki :

A • -12 <0

^J x² + 4x + 7

x² + 4x + 7b(x + 2)² ■» 3

f_dx_f^x*2-ll MX + 2)²+3 1 dx a dt |

--ifrći^^+c=i^misił^+c-

b,/^-=(V"^6<0    , U-V--|«A2_+C;

^J x³-6X4-13 [x² -6x + 13a(x-3)² + 4J ^j(x-3)²+4    ^2    2