MATEMATYKA104

198 IV. Całka nieoznaczona

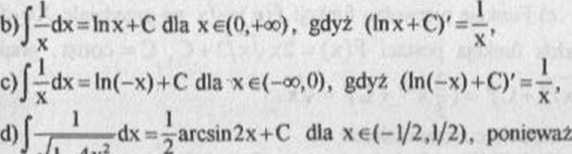
l-4x

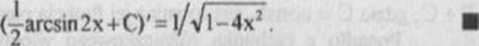
Funkcję f, dla której istnieje całka nieoznaczona na pewnym przedziale, nazywa się funkcją całkowalną na tym przedziale.

TWIERDZENIE 1.2 Każda funkcja ciągła na pewnym przedziale jest funkcją całkowalną na tym przedziale.

Ciągłość funkcji jest więc warunkiem wystarczającym jej całkowalności. Nie jest jednak warunkiem koniecznym. Można bowiem podać przykłady funkcji, które nie są ciągłe w jakimś punkcie przedziału, a mimo to są w^r nim całkowalne.

Wyznaczanie całki nieoznaczonej danej funkcji f - nazywa się całkowaniem funkcji f. Całokształt zagadnień z tym związanych nosi nazwę rachunku całkowego.

Z twierdzenia 1.2 wynika, że każda funkcja elementarna jest całkowalna w swej dziedzinie. Nic oznacza to jednak, że całka nieoznaczona dowolnej funkcji elementarnej jest rodziną funkcji elementarnych. Na przykład całki nieoznaczone

1

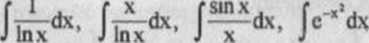
nic są funkcjami elementarnymi (nic wyrażają się za pomocą skończonej liczby działań arytmetycznych przez funkcje elementarne)

Z definicji całki    wynikają równości:

(1.3)    (Jf(x)dx)' = t(x; oraz JV(x)dx = f(x)+C

Na przykład

Z równości (1.3) wynika, 2c całkowanie i różniczkowanie są działaniami wzajemnie odwrotnymi.

WZORY BEZPOŚREDNIE I CAŁKA SUMY Każdy wzór F'(x) * f(x) rachunku różniczkowego prowadzi bezpośrednio do odpowiedniego wzoru na całkę niooaiaczoną;

(14)    F(x) = f(x)=>Jf(x)dx = F(x)+C.

Wzory w ten sposób otrzymane będziemy nazywać wzorami bezpośrednimi rachunku całkowego A oto tablica wzorów bezpośrednich

| Odx = C,

J^dx=ln|xj+C,

Ja^,d* ⁼ jna^a*^+C’

Jcosxdx = sinx+C,

f—y-dx = tgx+C,

^J cos x

f j Lin dx = arcsinx+C, ^J Vl-x²

J cosh xdx = sinh x+C,

[—j^-dx = tghx+C.

J cosh x

fx^adx=-!-rx^a+,+C, a*-l,

J    a +1

Je^xdx = e^x+C, sinxdx = -cosx+C,

f—V-dx = -ctgx+C_t ^J sin x

—!-_Tdx = arctgx+C_? l + x

J sinh xdx = cosh x+C,

—dx = -ctghx+C, sinh x

Zauważmy, że w'śród tych wzorów brak jest całek nieoznaczonych wielu funkcji elementarnych Na przykład brak jest całek Jtgxdx, Jlnxdx.

Metodę ich obliczenia poznamy później.

Z twierdzeń o pochodnej sumy funkcji i iloczynu stałej przez funkcję wynikają odpowiednie tw ierdzenia dla całki nieoznaczonej.

TWIERDZENIE 1.3 Jeżeli funkcje f i g są całkowalne na wspólnym przedziale, to suma f + g jest również funkcją całkowalną na tym przedziale i przy tym:

(1.5)    . J(f(x)+g(x) )dx = J f(x)dx+Jg(x)dx