kww mdm1

C.    jest rosnący'.

D.    jest malejący.

ZESTAW ZADAŃ PRZYGOTOWAWCZYCH POZIOM PODSTAWOWY

Zadania zamknięte (1 pkt)

1.    Funkcja f dana jest wzorem f(x) = -5x + 9. Które zdanie jest prawdziwe?

A.    Wykres funkcji f przecina oś y w punkcie (0, -5).

B.    Funkcja f jest rosnąca.

C.    Do wykresu funkcji f należy punkt P = (>/2; 1,93).

D.    Miejscem zerowym funkcji f jest liczba 1,8.

2.    Liczba -8⁵ jest równa:

A. 4 B. -4 C. -2 D. 2

3.    Rozwiązaniem nierówności [x + 6| < 7 są takie liczby x, które spełniają warunek:

A. x $ -13 lub x 2 1    C. x > -13 i x < 1

B. x > -13 i x < 1    D. x > -7 i x $ 7

4.    Jeżeli sinus pewnego kąta ostrego a wynosi to:

A.    cos« = |    C. cos« =

B.    cos«= _s    D. cos«=- ₅

5. Który ciąg jest ciągiem arytmetycznym?

a. = ■ +1    c-<•» = (;)"

B. b_n = n- - 9    D. d_n = (2n + 3)- - 4n²

6.    Okrąg o równaniu (x - 5)² + y² = 25

A.    jest styczny do osi y.

B.    jest styczny' do obu osi układu współrzędnych.

C.    jest styczny do osi x.

D.    nie jest styczny do żadnej osi układu wspólrzęd-nych.

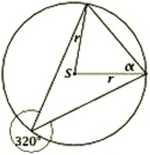
7.    Kąt a zaznaczony na rysunku obok jest równy:

A.    50"

B.    40"

C.    80"

D.    60

8.    Która prosta jest prostopadła do prostej o równaniu 3x -2y+ 9 = 0?

A.    3x- 2y + 4 = 0    C. 2x + 3y + 9=0

B.    2x-3y-t-9 = 0    D.-Jx-2y + 6 = 0

9.    Jeżeli przyjmiemy', że log 3 « 0,48 oraz log 200 = » 2,3, to log 600 wynosi w przybliżeniu:

A. 1,104 B. 2,78 C. -1,82 D. 1,82

10. Dane są liczby: a = 18* oraz b = (3v2) . Wskaż zdanie prawdziwe.

A.    Liczba a jest liczbą wymierną, a liczba b jest niewymierna.

B.    Liczba a jest większa od liczby' b.

C.    liczba b jest dwa razy większa od liczby a.

D.    Liczby a i b są równe.

11. W tabelce znajdują się dane na temat liczby książek, które przeczytali w ostatnim roku uczniowie pewnej klasy.

liczba przeczytany ch książek	0	1 3 4	5	7
liczba uczniów	1	3 6 7	13	2

Mediana tego zestawu danych wynosi:

A. 3,5 B. 5 C. 4,06 D. 4,5

12.    Funkcja y = 5(x + 3)“ - 4 jest malejąca w:

A. [-<»’, 3) B. {-cc--3) C. <-3;oo) D. {3;cc)

13.    Odległość środka symetrii pewnego kw adratu od jego wierzchołka wynosi 6. Obwód tego kw adratu jest równy^r:

A. 24y/2 B. 24 C. 48^2 D. 48

14.    Liczby: -4, x, -8 tworzą niemonotoniczny ciąg geometryczny' dla:

A. x = -6    C. x = 2

B. X = 4_v^;2    D. x = -4_v'2

15.    Cenę x pewnego towaru obniżono najpierw o 15%, a następnie o 696. Obecnie towar ten kosztpje:

A. x -    B. 0,79x C. 0,94x D. 0,799x

16.    Zbiór wszystkich miejsc zerowych funkcji f(x)= (x² -81)(3x -2) to:

A. {-9}    C- {f,9l

B. (-9,2,9}    D. {-9,2}

17.    Wartość wyrażenia x- y_v3 dla x = 4y'3 oraz y - -8v 3 wynosi:

A. 12^3    C. 4(v/3-6)

B. 4(6+^3)    D. 4_v^/3 + 8v6

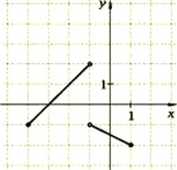
18.    Obok przedstawiono wykres funkcji f. Dziedziną funkcji f(x+13) jest zbiór:

A.    <-3;-l)u (-1; 1)

B.    <-17;-14) u (-14;-12)

C.    <-l6;-12)

D.    <10; 12) u (12; 14)

19.    Ciąg a„ = nr - 8n

A.    nie jest monotoniczny.

B.    jest niemalejący.

Zadania otwarte

20. (2 pkt) Kasia podjęła pracę w firmie kolportującej prasę. Zgodnie z umową otrzymywała 30 zl za każdy przepracowany dzień oraz 10 groszy za każdy egzemplarz sprzedanego czasopisma. W ciągu pierwszych dwudziestu dni pracy' udało jej się sprzedać 8346 egzemplarzy czasopisma.

a)    Oblicz kwotę, którą Kasia zarobiła w tym czasie.

b)    wycieczka, na którą chce pojechać Kasia, kosztuje 1800 zl. Ile gazet musiałaby sprzedać w ciągu miesiąca, który' liczy 22 dni robocze, aby na nią zarobić?

21.    (2 pkt) Znajdź wszystkie wymierne pierwiastki wielomianu: ll'(x) = 2x³ - 6x² - 16x + 48.

22.    (2 pkt) Wyznacz wszystkie liczby całkowite, które nie spełniają nierówności:

x² +- 2x - 15 > 0

23.    (2 pkt) Do wykresu funkcji f(x) = £-6 należy punkt P = (-1,4). wyznacz miejsce zerowe funkcji f.

24.    (2 pkt) Dziewczęta stanowią 60% wszystkich uczniów pewnej szkoły. Ile dziewcząt uczęszcza do tej szkoły', jeżeli wiadomo, że chłopców jest o 64 mniej niż dziewcząt?

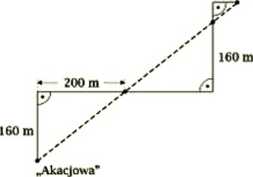
25.    (5 pkt) Na poniższym rysunku przedstawiono trasę przejazdu autobusu z przystanku „Akacjowa" do przystanku „Brzozowa”.

„Brzozowa”

Gdy autobus jedzie ze średnią prędkością 48,6 pokonuje tę trasę w ciągu jednej minuty. Jaka jest odległość w linii prostej między tymi przystankami? Wynik podaj z dokładnością do 0,1 m.

26. (6 pkt) Na poniższym ry sunku znajduje się fragment wykresu pewnej funkcji kwadratowej.

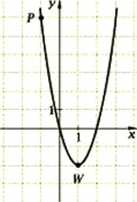
a)    Znajdź wzór tej funkcji w postaci ogólnej.

b)    wyznacz najmniejszą i największą wartość tej funkcji w' przedziale <-3;4>.

c)    Znajdź długość odcinka W P.