Lusniewicz zadania 3

0,226862

S5T= ~^t76    = 0,056715 (średni błąd losowy)

" 'ŁoL'_fy)-i

+-tb

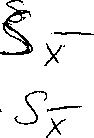
0,05 (deklarowany poziom istotności) Ś-n-1

S = 16 — 1=15 (liczba stopni swobody) /to,05;15/ = 2,131450 odczyt z tablic

Xi = 4,134375 - 2,131450 ■ 0,056715 = 4,013489 zł X£= 4,134375 + 2,131450 • 0,056715 = 4,255261 zł

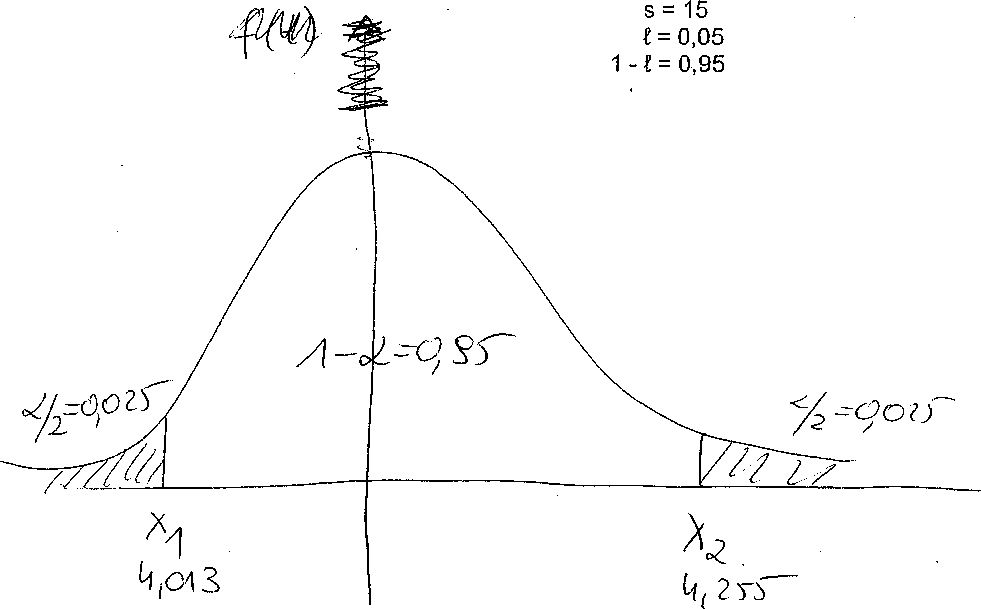
Interpretacja :

W oparciu o dane próby losowej 16 miast oszacowano końcówki (4,01 zł, 4,26 zł) 95% przedziału ufności dla średniej ceny we wszystkich miastach. Należy oczekiwać, że przedział z tymi końcówkami należy do podzbiorów przedziału ufności pokrywających szacowany parametr i że następuje to z prawdopodobieństwem 0,95. względna miara precyzji przeprowadzonej estymacji procesowej = 2,10 % co uzasadnia, że w danym przypadku (jest ono niższe niż 5%) wnioskowanie jest statystycznie bezpieczne.

Odp. d_'    __