img163

163

przedziale jego zmienności jest jednostajny, średniokwadratowy błąd kwantowania wynosi zatem (patrz zależność (1.4.10a))

163

e²

•h

(1.4.42a)

Odstęp sygnał - błąd kwantowania równa się

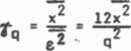
i jest wprost proporcjonalny do poziomu sygnału*. Podobnie jak przy przetwarzaniu bezpośrednim, szerokość przedziału kwantowania nie może być dowolna; naszym ograniczeniem jest obecnie nierówność (1.4.40)", a w przypadku sygnału harmonicznego x(t) = acosco^t jej odpowiednik (1.4.41). Po odpowiednim podstawieniu otrzymujemy

r_q< 3t₀

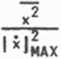
(1.4.43a)

oraz dla sygnału harmonicznego

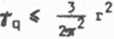
(1.4.43b)

Nie będziemy w tej chwili porównywać modulacji PCM i DM oraz DPCM pod względem wielkości odstępu sygnał - błąd kwantowania. Problemem tym zajmiemy się w podrozdziale 1.4.4, gdzie dodatkowo uwzględnimy wpływ odbiornika.

Znany jest szereg odmian podstawowej wersji modulacji DM [31, 34, 26]. Polegają one na wtrąceniu w zasadniczy schemat układu przetwarzania (1.4.13a) dodatkowych układów liniowych. W modulacji D £H (Delta Sigma Modulation) sygnał oryginalny jest wstępnie całkowany, co pozwala przetwarzać sygnały szybkozmienne. Modulator DMDI (Delta Modulation Oouble Integration - modulacja delta z podwójnym całkowaniem) zawiera w pętli sprzężenia zwrotnego dwa układy całkujące, zazwyczaj z lokalnym sprzężeniem zwrotnym. Tak rozbudowana pętla sprzężenia zwrotnego znacznie lepiej aproksymuje sygnał przetwarzany, chociażby dlatego, że przebieg sygnału aproksymującego jest liniowy, a nie schodkowy. W efekcie uzyskujemy wzrost odstępu sygnał - błąd aproksymacji. Zuważmy, że przedstawione modyfikącje można wprowadzić równocześnie. IPpraktjcc nie znalazły one większego zastosowania, gdyż wyraźnie lepsze efekty uzyskuje się w adaptacyjnych wer-

•Zauważmy, że nic nie stoi na przeszkodzie, by zależność (1.4.42) stosować również w przypadku modulacji DPCM.