skanuj0043

■danie 21. (9 pkt)

r okrąg o promieniu 5 cm wpisano trapez tak, że jedna z jego podstaw jest średnicą tego sręgu. Wysokość trapezu ma długość 4,8 cm.

Oblicz obwód trapezu.

• Czy w ten trapez można wpisać okrąg? Odpowiedź uzasadnij.

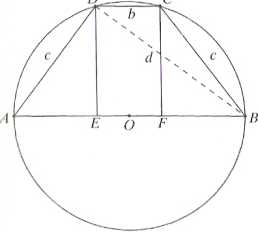
\AO\ = \OB\ = 5 cm \DE\ m \CF\ =h = 4,8 cm \BD\ = d \CD\ = b b > 0, d > 0

2p - obwód trapezu ABCD \aptzABCD jest trapezem równoramiennym, więc \AD\ — \BC\ AD\ = \BC\ =c,c > 0

1ADB - kąt wpisany w okrąg oparty na półokręgu => AD ± BD Lp*|s \AB\ ■ \DE\ = |riS'4,8 = 24[cm²| ^:

*UABC ~ c < d

\^cd = 24 P = 48

i ABD: c² + d² = 10², 0 < c < d cd = 48 C² + d² = 100

/ ⁺ (?)² = ¹⁰⁰ •⁴ - 100c² + 2304 = 0 oprowadzamy zmienną pomocniczą i² ■= t, t > 0 ^a - 100* + 2304 = 0 % * 10000-9216 = 784 JE =28

100 - 28 2 $1	V	, 100 + 28 „„ §? 2 -^64
c^2 = 36	V	II o\ -P-
c = -6 V c = 6	V	cc 1 II > oo II O
nie spełnia		nie spełnia
założenia c > 0		założenia c > 0

Z założenia c < d, więc rozwiązaniem jest para liczb

c = 6 d = 8

tiADE'. 6² = 4,8²+ |^JP:

|/4£|² = 36-23,04 \AE |² = 12,96 |/4£| = 3,6

ll iipcz/45CD jest trapezem równoramiennym, więc:

|C7)| - 10-2- 3,6 = 2,8

2p = 10 + 2,8 + 2 • 6 = 24,8 Odp.l Obwód trapezu jest równy 24,8 cm.

I*) Aby w trapez ABCD można było wpisać okrąg musi być spełniony warunek: \AH\ + \CD\ = \AD\ + |BC|

\AH\ + \CD\ = 10 + 2,8 = 12,8 \AO\ + \BC\ ■ 6 + 6 = 12 \Alt\ + |GDj1 * \AD\ + |BC|

Oiłp W len trapez nie można wpisać okręgu.