P1010603

110 Równanie falowe. Fala płaska

■ Równanie falowe dla fali EM wynika z równań Maxwełla Załóżmy, że mamy I ośrodek neutralny - tj. taki, w którym nie ma nadmiarowych ładunków (p =0); I nieprzewodzący - tj. taki. w którym pole elektryczne E nie powoduje powstania prądu I (J - 0); o wzlędnych przenikałnościach e i ji. I równanie Maxwella ma wtenczas postać I

^Vx^⁼-^⁼-woy-

Obliczmy teraz rotację obu stron powyższego równania Korzystając z 0 równania I

—>    .    "ł —*

Maxwella (dla j = 0 ) i równania materiałowego D = eso £ otrzymujemy

VxVx£«Vx WOTrJ " “ W*0*(^{v x}    ~ Wos(“0^-J ■ -EEoMPo^f

Lewą stronę powyższego równania możemy przekształcić następująco Vx Vx£-V[V£j-(VV)E«*V[V£j-AE.

Zgodnie z m równaniem Maxwe!ła V E = 0, a więc V(Vi?) = 0“ ostatecznie prowadzi ■4

do równania falowego na E w postaci ogólnej

_lv² dt²

Wychodząc z 0 równania Maxwella i postępując analogicznie otrzymujemy podobne równanie falowe na składową magnetyczną H pola elektromagnetycznego. Równanie falowe w postaci ogólnej (z Laplasjanem) jest ono równaniem wektorowym na funkcję E = E(y,y,;,t). Po zapisanu wektora natężenia pola elektrycznego za pomocą współrzędnych kartezjańskich E =(E_x.E_y.E_:) powyższe równanie falowe w postaci ogólnej rozpada się na trzy równania dla poszczególnych składowych składowych natężenia poła Np. dla składowej E mamy

ZpĘy d²Ey d²Ey | CpEy

^Ey~ dz² + dy² + ds² "V² dt² ' .

Jeżeli składowa E_y zmienia się tylko w zależności od z, a w kierunku y i z jest stała, (fala płaska) powyższe równanie upraszcza się do postaci ćP-Ey    i d²Ey

dz²    v² dl²

czyli otrzymaliśmy równanie dla składowej elektrycznej fali rozchodzącej się w kierunku osi OX.

■ Monochromatyczna plaska fala elektromagnetyczna, jest szczególnym przypadkiem płaskiej fali elektromagnetycznej, w której wektory E i H drgają w sposób harmoniczny z określoną częstością. W każdym punkcie przestrzeni trójka wektorów E, H i k tworzy prawoskrętny układ kartezjański. Związek pomiędzy amplitudami natężenia pola elektrycznego i magnetycznego otrzymujemy z podstawienia równań pola elektromagnetycznego do I i D równania Maxwella, które tutaj redukują się do postaci tty    9H_:    ÓHz    ^d£y

a7 = -W»o-a7-;    ~dx⁼~^eeo-gf- •

Spełnienie powyższych równań jest możliwe, gdy Eq = Hq Tppó.

Fale elektromagnetyczne

111

_ ■

« Elektromagnetyczna (EM) fala płaska

równanie falowe dla fali elektromagnetycznej rozchodzącej się »zdłui osi OX

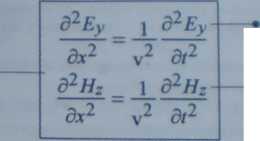
natężenie pola elektrycznego fali EM

natężenie pola magnetycznego fali EM

i prędkość światła w próżni c =

prędkość fazowa fali elektromagnetycznej! w ośrodku

v=

ÓW*0    JżTi

-♦ współczynnik załamania ośrodka

75.1 Monochromatyczna płaska fala EM

j» amplituda natężenia pola elektrycznego

Ey = £qcos(co/ -    + 5)_

yfts i/()COS((D/ - fcc + 5)

» jednakowa fiaza początkowa

• amplituda natężenia pola magnetycznego

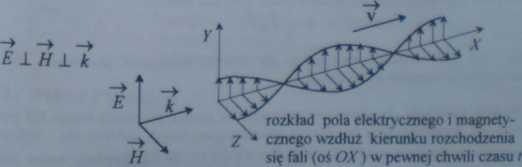
równania pola« elektrycznego i magnetycznego monochromatycznej fali EM

-EoJEefi =;#0i/PPÓ

związek pomiędzy amplitudami natężenia w-pola elektrycznego i magnetycznego