siecid

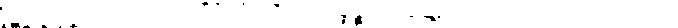
torów idealnych przy n - I,n = 2,«*=5i/: = 10 spo;*    ^

(7.17), przy czym na osi odciętych odłożono czas względny k_st.

Postać krzywych, przedstawionych na rys. 7-9_t potwierdza słuszność przyto-czonych wyżej rozważań, Przy przejścia od łańcucha zawierającego 5 reru la torów do łańcucha o 10 regulatorach, wzrasta szybkość zmiany wielkości reguk ^rti na wyjściu łańcucha, a także ilość ekstremów krzywej i liczba punktów jej przecięć, z osią czasu. W tym czasie wielkość pierwszego ekstremum wzrasta bardzo nieznacznie. Można pokazać, że wielkość pierwszego ekstremum, a odpowiednio i maksymalna wielkość przeregulow-ania na wyjściu łańcucha regulatorów idealnych przy n zmierzającym do nieskończoności jest ograniczona.

Uprościmy wyrażenie (7.17), zastępując w nim k_st przez x, wówczas dostaniemy

K\x) =

X    X²

p+ęf-1 *

1!

2!

-i

('I-D!

Teraz znajdziemy pierwszą pochodną tego wyrażenia:

dx

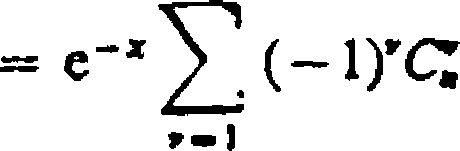
x'-¹ (>-!)!

Z ostatniego wyrażenia może być określona wielkość początkowej szybkości regulacji, która ma miejsce dla / = 0.

W ten sposób:

dh_m[x(t)} dt

d

m

Po

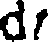
gdzie: p₀ — wielkość początkowego uskoku poziomu, a dx = k_tdt, co przy : - 0 daje

óp(t)

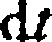
IsO

Po k_I n

W ten sposób początkowa szybkość regulacji na wyjściu łańcucha regulatorów idealnych jest wprost proporcjonalna do amplitudy uskoku poziomu i liczby urządzeń ARP w łańcuchu.

Rozpatrzony wyżej sens fizyczny procesów przejściowych jest słuszny i dla łańcucha idealnych regulatorów poziomu. W przypadku rzeczywistych regulatorów poziomu proces przejściowy na wyjściu łańcucha posiada również charakter oscylacyjny.

7.3.2

CHARAKTERYSTYKI PRZEJŚCIOWE UKŁADÓW REGULACJI DYSKRETNEJ

Na rys. 7-10 przedstawiono schemat strukturalny urządzenia ARP z regulatorem impulsowym, w którym wydzielono następujące układy: układ nielinio-

268