skanowanie0062 (2)

Przykład 6.13. Jednorodny walec o masie m kg i promieniu podstawy r m toczy się bez poślizgu po równi pochyłej nachylonej pod kątem a do poziomu (rys. 6.13). Współczynnik tarcia tocznego walca o równię wynosi/. Jaką prędkość będzie miał środek walca po przebyciu drogi s, jeśli walec puszczono bez prędkości początkowej?

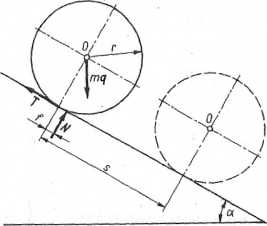
Rys. 6.13. Do przykładu 6.13

Rozwiązanie. W chwili początkowej prędkość liniowa i kątowa walca są równe zeru, zatem początkowa energia kinetyczna

E_t-0

Końcowa energia kinetyczna walca wynosi

E₂ “ ymi>²+y/o)²

gdzie

j _ mr²

Pracę wykonują siła ciężkości i moment Nf W= mgsńnu—Nfcp

Po uwzględnieniu zależności między prędkością liniową v a kątową (0, drogą s i kątem obrotu <p oraz wartości siły normalnej N

^{S    V}    xr

(o = —,    (o = —.    N = mg cos a

r    r

otrzymamy

Stąd

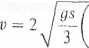
f

sina-— cos a

Przykład 6.14. Układ pozostający w płaszczyźnie pionowej składa się z korby AB o masie m₁ kg, zamocowanej przegubowo w punkcie A, oraz krążka o masie m₂ kg i promieniu r m. Krążek może toczyć się bez poślizgu po wewnętrznej powierzchni nieruchomego walca o promieniu R m (rys. 6.14). Jaką prędkość v_B osiągnie środek masy krążka w chwili jego przechodzenia przez najniższe położenie, jeżeli w położeniu pionowym korby miała ona prędkość kątową (

c

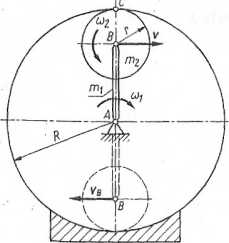
Rys. 6.14. Do przykładu 6.14

Rozwiązanie. Energia kinetyczna układu w położeniu początkowym

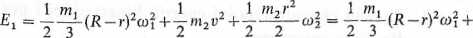
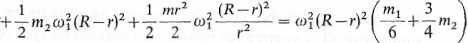
gdzie:

v = co₁(R-r),

0)₂ — o)

R-r

r

10* 147