skanowanie0060 (2)

Rozwiązanie. Dynamiczne równania ruchu płaskiego krążka toczącego się bez poślizgu po równi pochyłej (rys. 6.10): .

1.    ma_t — Sj — T— mgsina

2.    m 0 ig N—mg cos a

3.

-_fil = Tr-Nf

Dynamiczne równanie ruchu obrotowego krążków wzajemnie połączonych o środku w punkcie O

4.

-+

2m(2r)²

e₂ M 4,5mr² e₂ = M + S₃ • 2r+S₂r—S₁ • 2r

Dynamiczne równania ruchu płaskiego krążka ruchomego o środku B:

5.    ma₂ = S₄.+mg — (S₂+S₃)cosl5 ^mr2 „ c c

6.    ~2~h = S₂r-S₃r    ...

Dynamiczne równanie ruchu ciężarka C

7.    ma₂ = mg—Są.

Równania więzów układu mas mają postać:

8.    fl, =8

9.    — e₂ ■ 2r

10.    e₂-2r = a₂+e_zr 11. a, — e,r+fi,r

m m

e, m

16	M	48	.n _L	32
83	mr	83	y •	83	r
12	M	36	. fi 4.	24	£
83	mr	83	0T	83	r
Oli			^fll
r ^!	i ®2	“'	w	t	‘3 ^=

4 r

Po rozwiązaniu układu dziesięciu równań otrzymamy -(r sin a—/cos a)

Przykład 6.11. Na rysunku 6.11 pokazano układ trzech krążków o masach m i promieniach r oraz dwa ciała A i B o masach m. Ciało A porusza się po chropowatej równi pochyłej o współczynniku tarcia ślizgowego n. Do tego ciała przyczepiono jeden koniec liny, którą przerzucono przez stały krążek o środku O, i owinięto ruchomy krążek o środku 0₂. Drugi koniec tej liny zamocowano w punkcie C. Do środka 0₂ krążka ruchomego przyczepiono drilgą linę, którą owinięto krążek ruchomy o środku 0₃. Do środka 0₃ krążka ruchomego zamocowano na linie ciało B. Napisać równania ruchu i równania więzów.

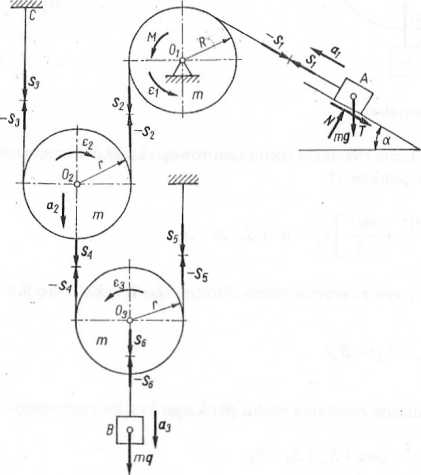
Rys. 6.11. Do przykładu 6.11

Rozwiązanie. Dynamiczne równania ruchu ciała A:

1.    ma₁=S_l — T—mg sina

2.    m-0 = N—mg cos a

W przypadku tarcia ślizgowego rozwiniętego

3.    7= fiN

143