skanowanie0058 (2)

Przykład 6.8. Na rysunku 6.8a pokazano układ czterech kół i ciężar P. Koło o masie m toczy się bez poślizgu po równi pochyłej o kącie pochylenia a, a współczynnik tarcia tocznego wynosi /. Stały moment M N • iti jest przyłożony dp.koła obracającego się względem osi O. Napisać równania ruchu i zależności między przyspieszeniami liniowymi i kątowymi.

Rozwiązanie. Dynamiczne równania ruchu płaskiego koła poruszającego się po równi pochyłej (rys. 6.8b):

1.    ma_l=S_l — T—mgsina

2.    m*0 = N—mgcosa.

3- —2~s₁ = Tr—Nf

Dynamiczne równania ruchu kół wzajemnie połączonych o środku w punkcie O (rys. 6.8b):

4.    4m-0 = R_0x—SjCOsa

5.    4m-0 = R₀y—Amg—S₂ — Sasina

3m(3r)^:

A*

mr

e₂ = S₂r+M—S_l-3r

Dynamiczne równania ruchu płaskiego koła ruchomego o masie 2m (rys. 6.8b):

7. 2 ma₂ = 2 mg—S₂ — S₃ + S_Ą

o 2m(2r)²

8. —2—^e3 m

—S₂’2r+S₃-2r

Dynamiczne równanie ruchu ciężaru P P

9.    —a₂ = mg-S4

y

Zależności między przyspieszeniami liniowymi i kątowymi (równania więzów):

10.    flj m s₂r

11.    6_tr = e₂-3r

12.    a₂ = — 8₂r

2    2 ²

13.    e₂r = a₂+e₃-2r

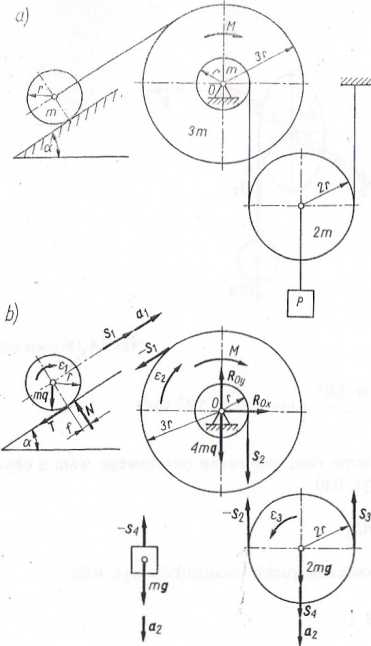
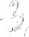
Rys. 6.8. Do przykładu 6.8

Przykład 6.9. Ciężarek A o masie m kg zawieszono na jednorodnej i nierozciągliwej linie. Lina jest nawinięta na krążek o masie 2m i promieniu 2r. Z krążkiem tym jest połączony sztywno drugi krążek o promieniu r i masie m, na który nawinięto jeden koniec drugiej liny, przerzuconej przez stały krążek o masie m i promieniu r oraz ruchomy krążek o masie 2m i promieniu 2r. Drugi koniec tej liny zamocowano sztywno w punkcie B (rys. 6.9). Stały moment M N • m jest przyłożony do kół wzajemnie połączonych o środku w punkcie O_v Do środka koła ruchomego (w punkcie 0₃) przymocowano ciężarek C o masie m. Napisać równania ruchu i równania więzów umożliwiające wyznaczenie napięcia w linach i przyspieszenia liniowe oraz kątowe poszczególnych elementów układu.

Rozwiązanie. Dynamiczne równanie ruchu ciężarka A (rys. 6.9)

1. ma_l = mg—S_l