skanuj0033
Slajd
7

UKŁAD REGULACJI TURBINY BEZ UPUSTU REGULOWANEGO
równanie charakterystyczne
l + Go(s) = 0
z ostatniego równania jeżeli jeden z pierwiastków spełnia równanie charakterystyczne
G0(s,) = -l + jO
to wyznacza tzw. punkt krytyczny PK(-1, j(ł)
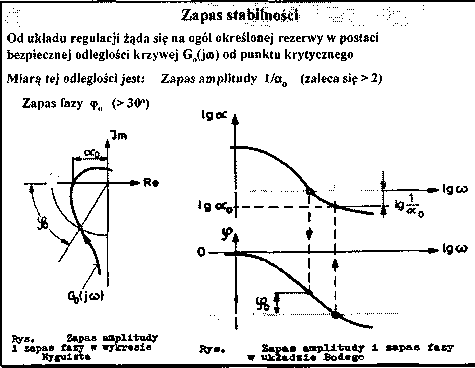
Kryterium Nyquista, lewej strony
STABILNOŚĆ UKŁADÓW LINIOWYCH

Układ regulacji po zamknięciu jest stabilny, jeżeli punkt krytyczny PK(-1, jO) leży po lewej stronie charakterystyki częstotliwościowej układu otwartego
Slajd
2
Układ jest stabilny, jeżeli wszystkie pierwiastki równania charakterystycznego majjj części rzeczywiste ujemne.
Kryterium lN'yquista (kryterium graficzne)
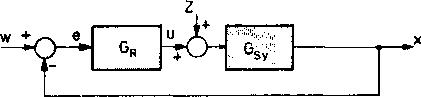
Rys, Schemat blokowy obwodu regulacji Równanie obwodu regulacji
x(s)-(1 + Gr-Gs) = w(s)-Gr-Gs+z(s)-Gs lub x(s)-(l + G0) = w(s)-G0+z(s)-Gs
G„ = Gr ■ G ^ - transmitancja układu otwartego
Slajd
5
36
Wyszukiwarka
Podobne podstrony:
skanuj0005 Slajd 13 Slajd 14 Slajd 1Funkcja regulatora Regulator wg określonego prawa regulacji zami
skanuj0020 Slajd 17 Slajd 1 Układy regulacji przerywanej (dyskretnej) 22
Schemat układ regulacji SCHEMAT UKŁADU REGULACJI H Aa < JT * * —Ut J r i i i Ur- układ regul
68833 skanuj0036 (23) Układ nerwowy Osoba uzależniona psychicznie nie potrafi bez pomocy z zewnątrz
VII. Obieg pracy turbiny Główny zawór odcinający, dławienie izentefpowe Układ regulacji 4.5 3 I 3’
Ryc. 9.17. Układ regulacji z jedną pętlą ęnftOM zwrotnego; y - parametr regulowany układu, A - układ
skanuj0017 IH układ 4£. /fi. ZOOZ. ^ ko/o*. Karycrcf/ifewJ rr/e-ZcU&opotfroz+i^P/L tfj f YCP/YĆ)
więcej podobnych podstron