skanuj0002

4

Transformator zasilany jest z. regulowanego źródła napięcia (autotransformator AT).

Przyrządy pomiarowe wskazują odpowiednio:

-    amperomierz: Im - prąd stanu jałowego

-    watomierz:    Pm - pobieraną z sieci moc czynną

-    woltomierz:    Um - napięcie zasilające transformator

Jeżeli jest to transformator idealny, to amperomierz wskazuje składową bierną prądu (Im = Ip), tzw. prąd magnesujący, watomierz Pm = 0, a woltomierz napięcie zasilające.

Wówczas

p

cos <p_m =-= 0

n

-— , czyli że

Oznacza to, że prąd ty jest przesunięty (opóźniony) względem napięcia o kąt (p\Q transformator idealny zachowuje się jak idealna indukcyjność.

W przypadku transformatora rzeczywistego watomierz wskazuje niewielką moc czynną pobieraną z sieci, która pokrywa straty mocy występujące w transformatorze. Moc ta jest równa:

PlO = A P,j ,0 + AP_F(1

gdzie: A P_um - straty w uzwojeniu pierwotnym A Ppe - straty w rdzeniu

Wobec tego

PjÓ ⁼ I 10^1 ⁺ &PFe    t¹)

Straty te wydzielają się w postaci ciepła w uzwojeniu pierwotnym i w rdzeniu transformatora. Straty w rdzeniu zależą od rodzaju blachy, z której wykonany jest rdzeń transformatora. Straty te można zmniejszyć przez dodanie niewielkiej ilości krzemu (do 4%). Mówimy wówczas o blachach transformatorowych „nakrzemionych”.

Straty w rdzeniu składają się ze strat na hislerezę AP_H (przemagnesowywanie) oraz strat na prądy wirowe APw. Straty te można wyrazić przy pomocy zależności

/SP_Fe = /SPp + AP_W = k _H ■ j ■ B}_n + k_w • f² ■ B?„

gdzie: k_H , kw - stale współczynniki f    -częstotliwość

B„,    - wartość maksymalna indukcji magnetycznej

Jeżeli częstotliwość f = const, to możemy napisać

&PFe ⁼ [^nf ⁺ hvf² )' Pm -k-B²m

Ponieważ indukcja magnetyczna B_m jest proporcjonalna do napięcia (B_m~Ui), wobec tego mamy

tsPpe ~ hfeU\

Straty te są proporcjonalne do kwadratu napięcia. Przebieg tych strat można wyznaczyć z zależności (1)

^PFe = P\0 ~¹\d^R\

Zmieniając napięcie zasilające transformator dokonujemy pomiarów mocy P_t0 i prądu I|₀ i obliczamy straty w rdzeniu i wykreślamy w zależności od napięcia (APp_P = f (Ui) ). Przebieg tych strat pokazano na rys. 3.

Ze względu na to, że rdzeń transformatora jest składany z blach, straty' na prądy wirowe są znacznie ograniczone i można praktycznie przyjąć, że straty w rdzeniu stanowią głównie straty na histerezę (AP_Kc = APh). Świadczy o tym następujący przykład Jeżeli rdzeń wykonany jest z blachy o grubości 0.35 mm o zawartości krzemu ok. 4%, to przy indukcji B_m = IT i częstotliwości f = 50 Hz poszczególne składowe wynoszą: APh = 87% APpe oraz AP_W = 13% AP_Fc. Wykres wskazowy stanu jałowego transformatora idealnego i rzeczywistego pokazano na rys. 4.

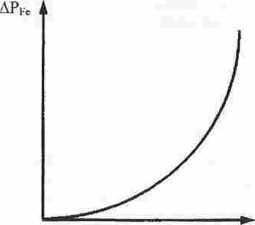
Rys. 3. Przebieg strat w rdzeniu

b) transformator rzeczywisty

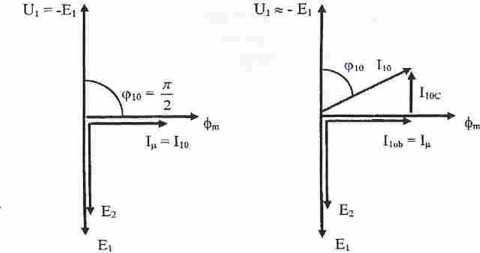
a) transformator i

Rys.4. Wykres wskazowy transformatora w stanie jałowymi

Jako wskaż odniesienia (wskaż rysowany poziomo) przyjęto strumień magnetyczny O,,,. Jest on

przesunięty (spóźnia się) w stosunku do napięcia U| o kąt n/2. Siły elektromotoryczne transformacji indukowane w uzwojeniach pierwotnym i wtórnym przesunięte są w stosunku do strumienia o kąt rr/2. W transformatorze idealnym prąd stanu jałowego posiada tylko składową bierną (I_)ob = I_łt). Natomiast w transformatorze rzeczywistymi prąd stanu jałowego I_w posiada dwie składowe: składową bierną (In*, = 1_M) oraz składową czynną (I_10c). Składowa czynna koc wynika ze strat mocy i jest w fazie z napięciem Uj. Składowa bierna 1₍, jest w fazie ze strumieniem i jest opóźniona w stosunku do napięcia o o kąt n/2. Prąd stanu jałowego I|₍₎ stanowiący sumę geometryczną wymienionych składowych, jest opóźniony w stosunku do napięcia o kąt <pi₀.

W stanie jałowym napięcie zasilające transformator praktycznie równoważy siłę elektromotoryczną indukowaną w uzwojeniu pierwotnym (tJi * -Ei).

4. ROZPROSZENIE STRUMIENIA MAGNETYCZNEGO

Prądy płynące przez uzwojenia transformatora wytwarzają przepływy (amperozwoje) powodujące pojawienie się strumieni magnetycznych. Każde z uzwojeń wytwarza składową strumienia głównego (<Pi2 i cf>₂₁) oraz strumień rozproszenia (0|, i <&#).

Składowe obu uzwojeń tworzą strumień główny skojarzony z obydwoma uzwojeniami. Wytworzone przez uzwojenia strumienie rozproszenia skojarzone są tylko z uzwojeniem, który' ten strumień wytwarza. Strumień rozproszenia zamyka się przede wszystkim przez powietrze (rys. 5.).