TOB13

Transformata tego napięcia

Uo(s) = — s

Impedancja widziana z zacisków otwartego łącznika przy zwarciu źródeł napięcia, wynosi

R(R + sL) 1    10s² + 27s + 10

^(S)_ 2R + sL ⁺ sC~ 2s(s + 5)

Prąd w gałęzi kondensatora

U₀(s)

m =

2{s + 5)

Z(s) s² + 2,7 s + 1 Napięcie na zaciskach kondensatora

Uc(s) = ^-I{s)+^Uc(0+)

2s + 10    5

s(s² + 2,7s + 1)    s

sC '' s Obliczamy pierwiastki równania

s² + 2,7 s -l- 1 = 0; Sj — —0,45,    Sj ⁼ —2,25

Przedstawimy napięcie na kondensatorze w postaci

U_c(s) =

2s + 10

s(s + 0,45) (s + 2,25) s Korzystamy z twierdzenia o residuach

ls+10    „1 f 2s +10

_S\__2s+10_ I ₌ I"_2s + 10    1

„L S(s + 0,45) (s + 2,25) J    _s^₀ |_ (s + 0,45) (s + 2,25) J

, f 2.s + 10    ]_    r ^2s+1° c«~l 1121

o,45 L^s(^s + 0,45) (s + 2,25) J _S___0>45|_s(s + 2,25) J

2s + 10

-0,45t

res

—-e^sf_| = lim I" f ^{S +}J?,. e^st~| - -1,36 e ^2,25t ,25) J _s_₂,2₅Ls(s + ⁰,45) J

■ — 2,25 |_^s(^s "I^- 0,45) (s + 2,25)

Ostatecznie napięcie na kondensatorze

u_c(f) = 10- U,24e-°’^45f- l,36e-^W5‘ + 5 = (15 - ll,24e-°’^45t + Uóe"²^) V

5.17. W obwodzie jak na rys. 5.17 w chwili t = 0 został otwarty łącznik W. Obliczyć przebieg napięcia u(t) na otwartym łączniku. Zastosować metodę Nortona. Dane: E = 30 V; R_l = R₂ = 10O; R = 5 fi; C = 10mF.

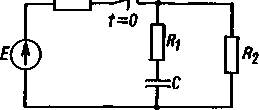
Rys. 5.17

Rozwiązanie. Prąd w gałęzi łącznika przed otwarciem wynosi

E    30

/ = --— = — = 2A

R + /?2    15

Impedancja operatorowa widziana z zacisków łącznika przy zwarciu źródła napięcia wynosi

Z(s) = R +

^r{^r- ⁺ 7c)

^{Ri + R2 +} Jc

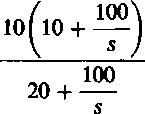
10 s + 300 s + 50

Napięcie na wyłączniku

U(s) = Z(s)I(s) =

2 10 s + 300 s s + 50

20s + 600 s(s + 50)

Przebieg czasowy tego napięcia

u(t) = (12 + 8e^_50‘) V

5.18. W obwodzie jak na rys. 5.18 w chwili t = 0 otwarto łącznik W. Metodą Nortona obliczyć przebieg napięcia u(t) na otwartym łączniku. Dane: £ = 30V;R₁ = 1Q;R₂ = 2Q; C = 2F.

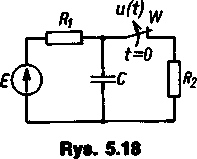
Rozwiązanie. Prąd płynący w gałęzi łącznika przed jego otwarciem wynosi

/ =

E

Ri + Ri

30

1+2

= 10 A