TOB14

Transformata tego prądu

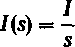
10

s

Impedancja operatorowa widziana z zacisków łącznika

Z(s) = R₂ +

^R‘Jc

^R' ⁺ JĆ

= 2 +

1

2s+ 1

4s + 3 2s + 1

Napięcie na zaciskach łącznika po jego otwarciu

U(s) = Z(s)I(s) =

4s + 3 10 2s + 1 s

40s + 30    20s + 15

s(2s+l) s(s + 0,5)

stąd

u(t) = (30 — 10e^_0,5‘) V

Napięcie to w chwili t = 0⁺, u(0⁺) = 20 V.

Rzeczywiście, w chwili tuż przed otwarciem łącznika napięcie na kondensatorze, równe napięciu na rezystorze R₂, wynosiło u_c(0“) = R₂I = 20 V. Z prawa komutacji wynika, że u_c(0~) = «_c(0⁺) = 20 V.

5.4. Metoda zmiennych stanu

5.19. W obwodzie jak na rys. 5.19a obliczyć prąd w cewce oraz napięcie na kondensatorze w stanie nieustalonym powstałym w wyniku zamknięcia łącznika w chwili t = 0. Zastosować metodę zmiennych stanu. Dane: £=100V;R₁ = R₂ = 50fi;L = lH; C = 10mF.

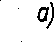
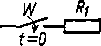
kp

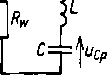
Rozwiązanie. Określamy prąd w cewce oraz napięcie na kondensatorze w stanie zerowym

fe(0-) = 0;

«c(0-) = 0

Wartości ustalone prądu i napięcia

ku = 0 A

“Cu =    —R₂ = -—50 = 50 V

Ri + R₂ ²    100

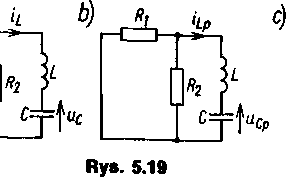
Schemat obwodu dla składowych przejściowych przedstawiono na rys. 5.19b, a po przekształceniu na rys. 5.19c. Dla tego schematu układamy równania

d t

R* kp + ^ucp + L

•L, =

d t

Wybieramy zmienne stanu

Formułujemy równanie stanu

Skąd po podstawieniu danych oraz

^dMcp = *i_P(0;    ⁼

d t

Xl p ~ ^Cp>

"dMCp"		0	1
d t			C
d iLp		1	Rn
_ d t -		L L	LA

^UCp

. kp.

pMOl ₌ [ 0    1001 U_p(tf|

UpWj L-¹ -25JU_P(t)J

x„ = Ax., przy czym A

r ° ^io°i

-[-i -25J

Rozwiązanie równania stanu

Xp = e x_p(0)

Określamy stan początkowy dla składowych przejściowych

/Lp(0⁺) = i_L(0⁺)-i_L„(0⁺) = 0

^Mcp(0⁺) = M_C(0⁺) - u_c„(0⁺) = -50 V Macierz stanu początkowego dla składowych przejściowych

M°)-["^So]

Obliczamy wartości własne macierzy A.