stany nieustalone str14

(107)

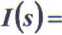
Z(s)

przy czym impedancja operatorowa gałęzi szeregowej R, C

z(s)=R + — ^V ’ sC

(108)

Następnie korzystamy z prawa Ohma w postaci operatorowej dla elementu C (tzn. z równania (80)) i w wyniku rozwiązania równań (107) i (80) dochodzimy do równania (1.97). Dalszy ciąg obliczania odpowiedzi czasowej na napięcie na kondensatorze nie ulega zmianie.

Stan nieustalony w gałęzi szeregowej R, C przy zwarciu

Rozpatrzmy obwód przedstawiony na rys. 11, w którym w chwili t = 0 dokonujemy operacji łączeniowej zmieniając położenie łącznika z poz. 1 na poz. 2. W wyniku tego gałąź R, C zostaje zwarta i jednocześnie odłączona od źródła napięcia stałego U.

Załóżmy, że zmiana położenia łącznika następuje bezprzerwowo, bezłukowo i w sposób natychmiastowy.

Warunki początkowe w obwodzie są niezerowe; w chwili t = 0 napięcie na kondensatorze wynosi U.

C

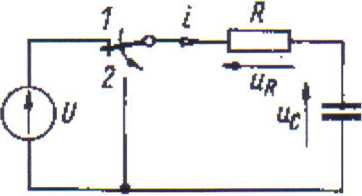
Rys. 11. Zwarcie gałęzi szeregowej R, Cprzy warunku początkowym niezerowym

Zgodnie z drugim prawem Kirchhoffa dla rozważanego obwodu przy położeniu łącznika w poz. 2 mamy

Ri(t)+ u_c(t)= 0

przy czym

^v ’ dt

Eliminując prąd w równaniu (109), otrzymujemy równanie względem napięcia na kondensatorze

RC—^{+    =} ®    (iii)

Dokonujemy przekształcenia Laplace’a równania (111). Warunek początkowy jest niezerowy: U(=(0)=U,

zatem otrzymujemy

(109)

(HO)

2007-01-10

14

TO/ES