stany nieustalone str10

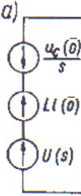
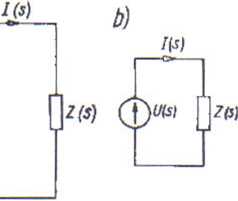
Rys. 7. Schemat operatorowy obwodu: a) przy warunkach początkowych niezerowych;b) przy warunkach początkowych zerowych

W równaniach (82) i (84) ważne jest to, że impedancja lub admitancja operatorowa wiąże ze sobą transformatę prądu I (s) oraz transformatę napięcia U(s) dwójnika.

Wielkość operatorową, określoną jako stosunek transformat napięcia i prądu dwójnika przy warunkach początkowych zerowych nazywamy immitancją operatorową. Wielkość    ta    może    być    stosunkiem    napięcia

do prądu lub prądu do napięcia. Immitancja operatorowa charakteryzuje w pełni własności tego dwójnika.

W układzie mającym n par zacisków każdej parze zacisków odpowiada pewien prąd i napięcie. Stosunek transformat dwóch wielkości związanych z różnymi parami zacisków n-wrotnika przy warunkach początkowych zerowych, nazywamy transmitancją operatorową.

Transmitancja operatorowa może być stosunkiem transformat prądów, transformat napięć jak również stosunkiem transformaty napięcia do transformaty prądu lub transformaty prądu do transformat napięcia. Transmitancja operatorowa jest oznaczona G(s), T (s) lub K(s).

Transmitancja operatorowa C(s) wiąże ze sobą dwa sygnały operatorowe, z których jeden -wejściowy oznaczymy przez U(s), a drugi wyjściowy przez Y(s). Zatem

y(s)=G(s)t/(s)    (90)

Równaniu (90) można przyporządkować schemat przedstawiony na rys.8 ujmujący współzależność transformat sygnałów wejścia i wyjścia poprzez transmitancję opisującą układ elektryczny w warunkach dynamicznych.

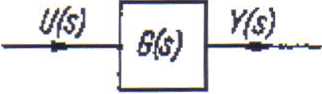
Rys. 8. Schemat jednonitkowy

Uwzględnienie warunków początkowych, jak pokazano na rys. 14.7a, jest szczególnie wygodne przy analizie obwodów złożonych. Umożliwia to wypisanie od razu równań w postaci operatorowej bez potrzeby każdorazowego formułowania równań oryginałów.

Dla tak określonego schematu można napisać prawa Kirchhoffa bilansu transformat prądów w węźle obwodu elektrycznego i bilansu transformat napięć w oczku.

Prawo Kirchhoffa bilansu transformat prądów w węźle ma postać

k

2007-01-10

10

TO/ES

(91)