stany nieustalone str12

(97)

stąd

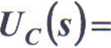
U + RCsU₀ s(RCs +1)

Równanie transformat (97) ma strukturę równania (65), przy czym L(s)=U + RCsUo,

M(s) = RCs+1.

Wobec tego, aby wyznaczyć odpowiedź czasową zastosujemy wzór (66). W rozpatrywanym przypadku    s<> = 0, S| = - 1/RC (jest to wynik rozwiązania równania RCs+l=Q).

Wypiszemy poszczególne wyrażenia występujące we wzorze (66)

Z,(o) = U; m(o)=1

L(s_t)=U-U₀; M'(s,)=RC

Zatem

U

C

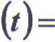
U

— + 1

u-u,

o

1

RC

RC

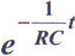
(98)

stąd ostatecznie

1

{u-u₀y«c

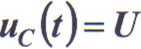
(99)

przy czym dla gałęzi szeregowej R, C stała czasowa

t = RC

(100)

czyli

u_c(l)=U-(U-U₀)e '

a przy warunku początkowym zerowym uc(0 ) = Uo = 0

(    --^

u_c{f) = U

(101)

(102)

t-e ^x \    J

Prąd ładowania kondensatora wyrażony równaniem (94) może być opisany następująco:

- przy warunku początkowym niezerowym

./X U-Ua ~

/(t) = —--e ^T

^w R

(103)

przy warunku początkowym zerowym ^V J R

2007-01-10

12

TO/ES

(104)