Temp001 tif

i 1 Podczas badania wysokości sadzonek okazało się, że sadzonek o wysokości do 2cm jest 10, od 2 do 4cm- 20, od 4 do 6cm-30, od 6 do 8cm - 40 i od 8cm do 10 cm - 60 sadzonek.	T/N
Obliczenie średniej wysokości sadzonek jako średniej arytmetycznej jest zasadne.
Obliczenie najczęściej spotkanej wysokości sadzonek jako dominanty rozkładu cechy jest zasadne.	^rr
Rozkład wysokości sadzonek jest rozkładem symetrycznym.	N
Mediana rozkładu wysokości sadzonek wynosi 6cm (Xj UŁŁ ( bo S2£ivt^ y[2£jiu,aXoLpJ ^ X. O-^juidź. tót , bo u&Le^i ^oiicŁMC, c) vO£ , fl<3ikIcuJ &vbuxe, a^w-mycŁlLU dj rIł ( ^ (ET- % , we > G 0-1 AO M iP H-6 i>0 Q)-% HO *■ me. %~A0 60 £ - /IGO w£ -=	N
12 Zapytano 20 osób o liczbę przepracowanych lat i otrzymano następujące informacje dwie osoby pracują krócej niż 3 lata, 8 osób pracuje krócej niż 6 lat, 18 osób pracuje krócej niż 9 lat. Dodatkowo wiadomo, że maksymalna liczba lat pracy w tej grupie nie przekracza 12 lat.	T/N
Rozkład liczby przepracowanych lat jest rozkładem symetrycznym.	N
Obliczenie średniej liczby przepracowanych lat jako średniej arytmetycznej jest zasadne.	T
Dominanta liczby przepracowanych lat jest większa niż 6 mniejsza niż 9 lat.	T
Mediana rozkładu liczby przepracowanych lat wynosi więcej niż 4 lata i mniej ^6 lat j C i 8-4 ; 0 o-b l 2 (0-3) 0-6 2 Q (i-dS a% ao (&-y ^ q \ nie, ! wdai a olaiwuclouaaue^) lo) tale cj tfidc , Toieb uosc ^ ^n.e&iO.(e 6-3 eh ^a pa.&diiak- 6 ~ 3	N

Dla cen towaru A wiadomo Xa=10z1, S.A.=2zŁ natomiast dla cen towaru B Xb=80USD; Sb~16USD.	T/N
Zmienność cen obu towarów mierzona wartością danego współczynnika zmienności jest taka sama.	T
Zmienność cen towarów A i B nie można porównać, ponieważ ceny mierzone są w różnych walutach.	N
Zmienność ceny towaru B jest większa od zmienności ceny towaru A ponieważ Sb jest większa niż wartość niż Sa.	N
Aby porównać zmienność ceny towarów A i B należy zastosować względną miarę zmienności. _ Xa-AOrJL %3\jso - AQ> USD ^ ^= ~t' $0 ^C^ÓA) (o,Sj) TAK, c)    nie- d)    Toio	T
T4W badaniu absencji 120 pracowników w I kwartale 2005 roku otrzymano X- Mx =Dx =5dni.Z ogółu korzystających ze zwolnień 30% pracowników nie pracowało tylko 1 albo 2 albo 3 dni. Kolejne liczby dni zwolnień brane pod uwagę w badaniu to (4,5,6) oraz (7,8,9).	T/N
Zgodnie z podanymi informacjami z ogółu korzystających ze zwolnień 30% pracowników nie pracowało tylko albo 7 albo 8 albo 9 dni.	T
Wartość klasycznego współczynnika asymetrii dla rozkładu liczby dni absencji wynosi 1.	N
Histogram liczby dni absencji jest figurą symetryczną.	T
Zgodnie z podanymi informacjami z ogółu korzystających ze zwolnień 40 pracowników przebywało na zwolnieniach w badanym okresie 4 albo 5 albo 6 dni. x =. Mx = Dx ~ uJdbai ^Yttdbt^uu SO ^ ~ A , £ , b nUl O O O ^ - H.S.G a 'toJo a fl/ ^ a a / ho /. - ^ c)    tale d)    wce. ^ ae m - 4S	t N

T5Obliczono wartość miar statystycznych charakteryzujących rozkład wartości cechy dla próby, w której rozkład wartości cechy jest rozkładem normalnym. Otrzymano następujące wyniki: X= 12, Mx= 6, Dx=9.	T/N
Wartość klasycznej miary kurtozy równa się 3.	T
Wartość wariancji wyznaczonej w tej próbie jest równa 0.	N
Około 69% jednostek z próby należy do przedziału (10,14), ponieważ średnia w próbie równa się 12, a odchylenie standardowe 2. toJ6 ( pojh^L uux<sv\ood loj 6^-0 cUjcl cae/re$u o) {akj X03- x - 5 < k+5 AX~ X <x /(O < x < AM	T
T6Na podstawie danych o produkcji przemysłowej w Islandii w 2003 roku obliczono, że w I kwartale wzrosła produkcja o 12%, a w II kwartale zmalała o 3%, w III kwartale wzrosła o 12% a w IV zmalała o 4%. Wszystkie zmiany mierzono do poprzedniego okresu.	T/N
Średnio w ciągu ostatnich 4 kwartałów produkcja przemysłowa w Islandii wzrosła o 4%.	T
Produkcja w III kwartale 2003 roku była wyższa około 5% niż w IV kwartale 2002 roku.	N
Produkcja w IV kwartale 2003 roku była wyższa niż w IV kwartale 2002 roku o więcej niż 16% a mniej niż 16,5%.	N
Produkcja w IV kwartale 2003 roku była wyższa niż w I kwartale 2003 roku o więcej niż 4,5% a mniej niż 5%. T IćH. A TT ktł 0, 31 nr ku. a , ^ Tu Wu 0t 36 a)    A ( aZi - 0,31* A, U-0,36 * Ml (M68ó) _ , (j/MY “ A, OM A, OM- A = C(M M f ^b)    X - U) ku icol X‘ A,U- : AtlA A-A,2A-0,2A (MAJOWIE q) a-a,/[Q,io zo/i&to ag,%o°/C wie <n Nit	V Kf
= A,°M4.g: a,a MW - ącMt M,as	£

A-hCHW - OOHW -3 q,a8^

i 7Z tego, że współczynnik korelacji liniowej pomiędzy cechami X i Y jest równy 1, zawsze wynika, że: I)    wskaźnik siły korelacji równy jest 1. II)    miara stopnia krzywoliniowości regresji równa się 0, III)    istnieją takie stałe a i b, że y - ax + b IV)    można stwierdzić, że między cechą X a cechą Y istnieje związek przyczynowo-skutkowy. Prawdziwe są własności 0 numerach:		T/N
Żaden z podanych wariantów.		N
Tylko II i III		N
Tylko Ii III Met t ko 9 ieŁ		!X W
Tylko III T TPiŻł -0 pcdba. UorCijCLCK &£tr50uxx u Nie ^ a f 0 ° w Tftk, — ^ foJkwL rrÓ»XiuXLu^ jjno&b&j wj tąk		N
18 Dokonano 80 pomiarów zużycia benzyny w 1/km (Y) przy różnej prędkości samochodu w km/h (X). Wyniki zestawiono w tablicy korelacyjnej. Na jej podstawie obliczono :		T/N
Kowariancję: 5,66	Wariancję zużycia benzyny: 1,96
Wariancję prędkości: 36,0	Średnią arytmetyczną wariancji warunkowych: Sj2 (x): 9,0
Wariancja średnich warunkowych zmiennej X jest równa 25		N
Współczynnik korelacji liniowej Pearsona między cechami X i Y jest równy mniej niż 0,7.		T
Wskaźnik korelacji prędkości (zm. zależna) od zużycia benzyny jest mniejszy niż 0,7.		N
Zmienność zużycia benzyny objaśnia zmienność prędkość w więcej niż 90%		N

^ T„ , -™3

^.o

~ \Tźz ~ C 'Su = Uw? * /i_tH

or** -

b, G6

')

'°a

• imsi¹

G*yi,M

Nlb

-- 0,G}5g

IAKj

52.

0,45MO -b 4t3,Mo)£

W ib

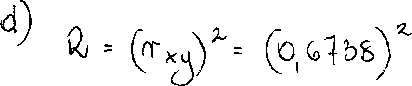
i -Cena akcji pewnej firmy w kolejnych notowaniach kształtowały się następująco w (zł): 28, 32, 38, 41,45. &	T/N
Trend liniowy jest dobrze dopasowanym do danych empirycznych modelem cen akcji.	T
Z modelu trendu liniowego wynika, ze cena akcji z notowania na notowanie rosła mniej niż 3,1 zł.	N
Z modelu trendu liniowego wynika, że cena akcji w okresie poprzedzającym pierwszą obserwację wyniosła mniej niż 2ł,5zŁ	N
Z prognozy otrzymanej na podstawie oszacowanej funkcji trendu liniowego wynika, że ceny akcji w pierwszym notowaniu po okresie obserwacji powinna wynieść około: 48,1 zł. ’ 1% , 'KI , b% , 44 ,W5 4 Q b 4 x = o) tok, bo mo2rU<x upwoż jswcTo b) ( x - 4,2,5 <*)	T
T10W browarze obliczono kwartalne wskaźniki sezonowośei(miary względne) produkcji piwa w latach 1991-2003, Oi=G,75, 02=45 i 03=0,60. Średnia kwartalna produkcja piwa wynosi 1000 hl (nie jestem pewien tej liczby..)	T/N
Przeciętna produkcja kwartalna w I kwartale wynosi: 1250 hl.	N
Przeciętna produkcja kwartalna w III kwartale wynosi: 2200hl.	N
Suma absolutnych odchyleń sezonowych w kwartałach od trendu wynosi 0.	BłT
Iloczyn względnych odchyleń sezonowych w kwartałach od trendu wynosi 4. 0/1 Ca.'0.M5 o^q<20 <V«= 2,2Z + qco-f v = 4 x = Aooo <£) Otf5*AOoo* Nie b)    0, GO • A000 - £00 Nlfc c)    lalo — dl) Tok, , -Q to .2,4 - ą# 5"	t M

1] i W 50 rodzinach przeprowadzono badanie ilości czasu przeznaczonego na pracę tygodniowo przez głowę rodziny (X, godz.) i wielkości tygodniowych dochodów (Y, w 1:ys. Zł). Na podstawie uzyskanych danych oszacowano linie regresji; “ 0,0łxi+0,02 xj = 90y) + 3	T/N
Współczynnik korelacji liniowej między zmiennymi X i Y wynosi 0,9	N
Wartość wskaźnika siły korelacji między zmienną Y (zależną), a zmienną X (niezależną) wynosi co najmniej 0,95.	T
Średni tygodniowy czas pracy głowy rodziny wynosi 48 godzin.	T
Zmiany czasu pracy w 99% objaśniają zmiany tygodniowych dochodów głowy rodziny.	N

T12Cena akcji pewnej firmy w kolejnych notowaniach kształtowały się następująco (zł): 25,23,21,20,18,15.	T/N
Trend liniowy jest dobrze dopasowanym do danych empirycznych modelem cen akcji.	T
Z modelu trendu liniowego wynika, że cena akcji z notowania na notowanie miała więcej niż 1,5 zł.	T
Z modelu trendu liniowego wynika, że cena akcji w okresie poprzedzającym pierwszą obserwację wynosiła mniej niż 26,5 zł.	N
Z prognozy otrzymanej na podstawie oszacowanej funkcji trendu liniowego wynika, że cena akcji w pierwszym notowani po okresie obserwacji powinna wynieść mniej niż 13,5 zł. ZS Zb, ZA .ZO.Ai . AS i ' ^1 1 ( Z ZA ći^ kay f bo w\o£Wxl Ux£lco ujkscxc Ó taJc , bo x = Z W/Ce. i bo 33 ■+ 2- = <2/-f	N

iĄjce_ ^ po poULc^.€uxa cl t b w kozi    wa. ^ozkoc

- *~ t t 2Q> ,52    b = ^

2C,^    = dd_t32

T i 3Tendencję rozwojową rejestrowania spółek prawa handlowego w Palarnie w latach 2002-2004 charakteryzuje funkcja trendu kwartalnego: Y; = 3t+ 10, i= 1,2,.....,12 Oszacowane wskaźniki sezonowości (miary względne) w poszczególnych kwartałach spełniają warunki: Oi=0,8 02=0,8 03=204	T/N
Wartość oczyszczonego wskaźnika sezonowości dla IV kwartału jest równa 0,8.	T
Absolutne odchylenie sezonowe liczby spółek dl III kwartału jest mniejsze od 15.	>T"
Teoretyczna liczba zarejestrowanych spółek w I kwartale 2006 jest większa od 60	T
Iloczyn względnych odchyleń sezonowych w kwartałach od trendu wynosi 1 0/1 =0,8 0i= 0,8 0^2'Otj X 0,8 + O, S" -t £* + x = 4 (bo treud kuaA+aiwo) 3x = i,HO / =3 ° x=0,g 0* = i-o,8 = A,bO Ow^O.8 a) WL ( pdb i<a_ Wj Tak , fcio tAO - ^ T ig. te ^ l~A~\ +>10" QA TAlc d) 0,5 ‘Ąb* /i ,60- 0K$ = 0,&& Mi£	N
T14Na kolejnych sesjach ceny akcji zmieniły swoją wartość w stosunku do ceny z poprzedniej sesji w sposób następujący +5%; +5%; -5%; +5% -5%; -5%. Cena akcji na ostatniej rozpatrywanej sesji w stosunku do pierwszej rozpatrywanej sesji:	T/N
Pozostała bez zmian	N
Wzrosła 0 1,25%	N
Żadna z odpowiedzi nie jest prawidłowa	rji
Spadła 0 1,25%	N

Cj, = A,06    C_n - A    0,SS^b    cena ^ada

uxwcu.ciiO«^, -> cewzL aka^C ua A aesjC - /tOD/i' C^C/i^^{-> 4} C_z - ^, oś    Cł ^    .

. _ . _a-    (bo uJotaiudŁ (e^k

^H ' T    (3 ^9WS - >1) • MO ~ ą T5/    ^er _A yj

^    ^/1'    cewa    o 0T5Z

c_& = 0,95

C* = 0,95

J 15W browarze obliczono kwartalne wskaźniki sezonowości (miary względne) produkcji piwa w latach 1991-2003: Oi=0,45, 02=0,65 i 04=1,45. Średnia kwartalna produkcja piwa wynosiła 5000 hl.	T/N
Przeciętna produkcja kwartalna w III kwartale wynosi 6000 hl.	N
Przeciętna produkcja kwartalna w I kwartale wynosi 2250 hl.	T
Suma absolutnych odchyleń sezonowych w kwartałach od trendu wynosi 0.
Iloczyn względnych odchyleń sezonowych w kwartałach od trendu wynosi 1.	N

o/|*a,4ę    o_z = o_k((,5 o_s = *

0,45-t 0,65 t v + /1, Mb - M

X- /l,45

/ O5-5000- /t₍4b-5COO^ 4.450 Nic t) 0* * 5030 - C\ HS • 0003 - i- 250 TAfc c) Ta \L , 5cutia    crf ck^leo cJo&oŁa+Utjcli    ^aus^e = O

tóy _ł 0_Ą * 0^ • O 5^Ł <3 9 =

= 0,95 * 0,65 ‘ 4,95 * 4,95 ' 0^64

TlóPodczas badania wysokości sadzonek okazało się, że sadzonek 0 wysokości do 2 cm jest 60, od 2 do 4 cm - 10, od 4 do 6 cm - 10, od 6 do 8 cm - 20 i od 8 do 10 cm - 80 sadzonek.
Obliczenie średniej wysokości sadzonek jako średniej arytmetycznej jest zasadne.	N
Obliczenie najczęściej spotykanej wysokości sadzonek jako dominanty rozkładu cechy jest zasadne.
Mediana rozkładu wysokości sadzonek wynosi blisko 7 cm.	rji
Rozkład wysokości sadzonek jest rozkładem symetrycznym.	N

W\£,

0-Ł	GO
■1-4	A0
	A0
-? 6-S	10
6- A0	^80 t -- MO
Cij nce. i	p^wiuuo ^5
b) tdk ,	1 iSJŁ. i*
c) tok;	^ \X2-QV \AO-
<4^ uic f	widać z da^jdi.

■)

o£0

-- Sf