FizykaII07201

67

sfcwy,.równoległej do osi długości pręta, mają ten sam ruch. co odpowiednie punkta osi samej, zatem można pręt uważać zamsze jako wiązkę równoległych rzędów punktów materyalnych. Dla tego chyżość przewodzenia fal w prętach można też wyrazić formułką, w onym paragrafie podaną,

która łatwo daje się sprowadzić do innych ilości, danych w doświadczeniu. Gdy bowiem zamiast e położymy moduł elastyczności pręta, t. j. ciężar Q.. który długość pręta l^mM grubego winien podwoić f§ 7J, a zamiast d jego masę, jednostce długości (i^?B) i jednostce przecięcia (1    odpowiednią, mamy ze

względu na to, że C = \/f— l, gdyż ilość e ma w istocie wartość modułu elastyczności, t. j.

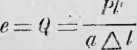
jeśli / długość pręta, a poprzeczne przecięcie jego, P zaś ciężar wystawia, który go ciągnieniem swojem o przedłuża,

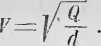
(II)

Lecz przyjąwszy /—Imi oznaczywszy głoską p ciężar pręta, mającego przecięcie a i długość jednego milimetra, głoską zaś 8 przedłużenie jego za pomocą tego ciężaru p, będzie widocznie

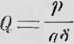
a znając ciężar gatunkowy .*,■ tego pręta, także, dla p = as,

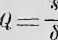
czyli dla tego, że w ogólności bezwzględny ciężar ciała równy jest iloczynowi z ciężaru względnego i z objętości jego, to jest p - rs (§ 105 T. I.), tudzież p = mg (§ 101), jeśli m masę jego. g zaś przyśpieszenie ciężkości ziemskiej w pewnem miejscu oznacza, zatem mg = vs, w naszym zaś przypadku według zrobionego wyżej przypuszczenia d wystawia masę jednostki objętości pręta, w mowie będącego, a więc wyraża ciężar takowego pręta, mającego 1 metr długości, a lmm w przecięciu, nareszcie