FizykaII16001

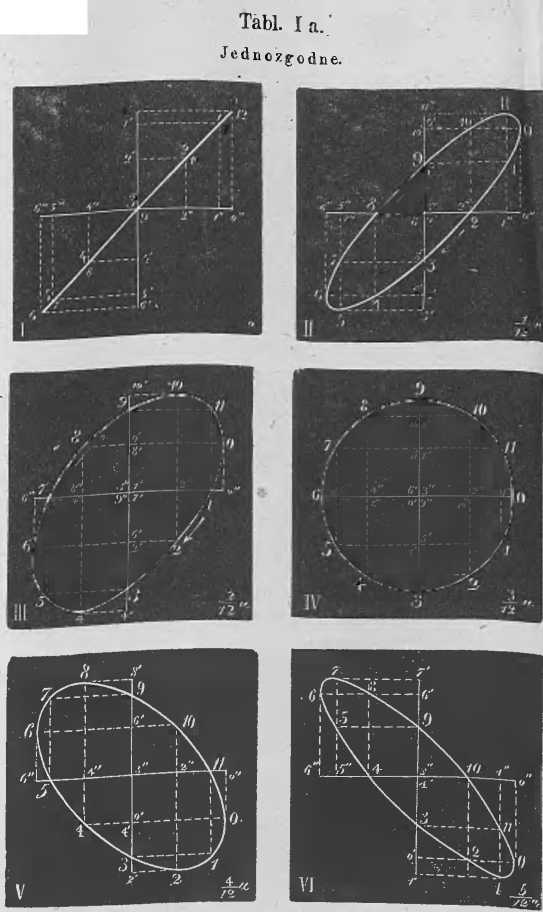
Uwaga. Figury Lissajouba na tabl. I a są geometryczne-mi miejscami zrównania 2) w § 83 T. I i II) w § 8 T. II, które wystawia elipsę, a nie parabolę lub hiperbolę, gdyż według zasad analitycznój geometryi zrównanie drugiego stopnia,- mające formę Ay¹ -j- Dxy -)- Cx² -j- Dy -(- Ex -j- F — o odpowiada elipsie, hiperboli lula paraboli, jeśli jest odnośnie B¹ — 4AC<£,>, lub = o;

a żę odmianą elipsy jest koło i linia prosta, więc w onym § 83 po wyrazach: swój znak jakości, należy położyć opuszczone zdanie: chyba że on prostolinijny.

Ogólną teoryę matematyczną figur na tych trzech tablicach rozwinął prof. Dr. Strzelecki ¹) Wziąwszy za osie współrzędnych same kierunki drgań składowych, nachylonych ku sobie pod kątem —j- y, i oznaczywszy przez a i a amplitudy,

x y

przez T i T czasy, a przez n i n względne liczby tych drgań,

x y    x y

licząc czas fazy każdego od chwili największego wychylenia na stronie dodatnich współrzędnych, zwykłym trybem składania takich dwóch ruchów z różnicą S czasów fazy, przyszedł do wyrażeń matematycznych, z których okazuje się:

1)    Źe, gdy n = l i n= 1, figurą wypadkowego drgania

x    y

jest elipsa; ta zaś staje się odcinkiem linii prostćj, skoro jest

T /    T’\

ii—o, a linią kolistą, jeśli S — — I 1— — )i zarazem a—a.

- \    n /    x y

Niekoniecznie więc kąt j, musi być prostym (ob. § 83), aby z dwóch ruchów składowych powstała linia kolista jako figura wypadkowa.

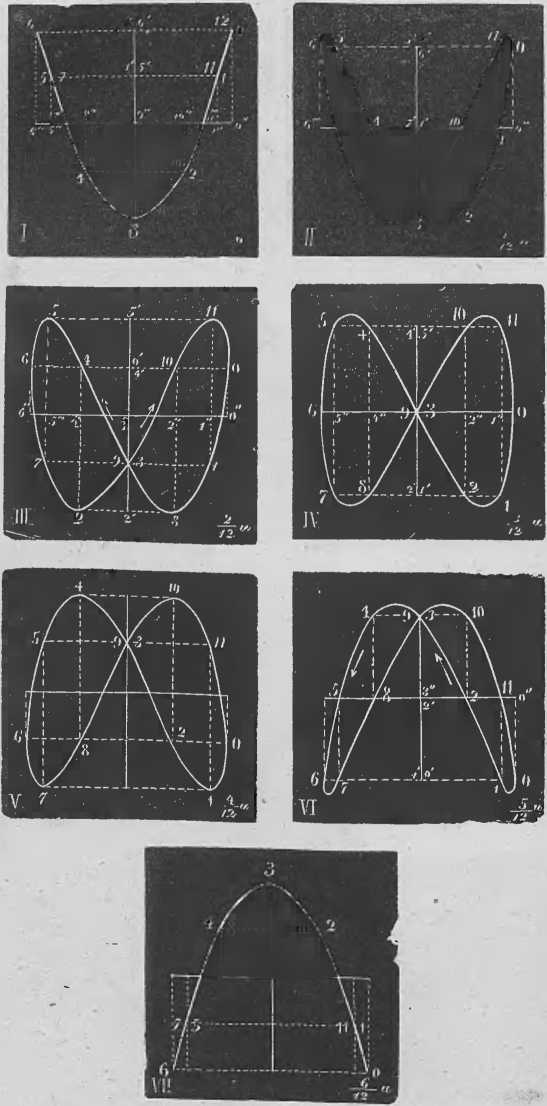
2)    Jeżeli n—2 a n — 1 i d' — o, krzywicą wypadkowe-

x    y

go drgania jest parabola drugiego stopnia.

3)    Zrównanie krzywicy wypadkowego drgania jest w ogólności względem x zawsze 2n-ego, względem y zaś 2n-ego stop-

y    x

nia. On zmniejsza się o połowę odnośnie do obu tych ilości, skoro ó — o.

4)    Wierżchołków krzywicy wypadkowego drgania, czyli tych jćj punktów, których styczne są równoległe do osi współrzędnych jest 2n odnośnie do x, a 2n odnośnie do y.

y    x

5)    Węzły tych krzywic, czyli punkta wzajemnego przecinania się ich gałęzi, leżą podobnie, jak wierzchołki ich, to na równoległych do osi x, to na równoległych do osi y. Ilość pierwszych wynosi n (n — 1\, gdyż na kazdćj z n — 1 równole-

y \x )    X

głych do osi x jest ich « ; ilość zaś drugich n. (n — 7\ , bo na

y    X \y J

każdćj z (n — A równoległych do osi y masz ich n.

\u )    x

(do są. l&ł)

Tabi. I b.

Tflbl- I C.

Ton zasadniczy i jego oktawa.

Ton zasadniczy i kwinta.    Ton zasadniczy i duodccyma.

1

Pamiętnik swej jirzeslai wideńsŁiej Akademii umiejętności w óru-dniu 1806. r.