1954 Geometria 308

4. Objem ihlana

Najpry dokażeme pomocnu vetu, na ktoru sa budeme pri stanoyeni objemu ihlana odvolava£.

Nech je dany ihlan o vrehole V, o podstave v rovine a; nech P je pata yyśky spustenej z V na a. Rcmna y je rovnobeżna s rovinou x,

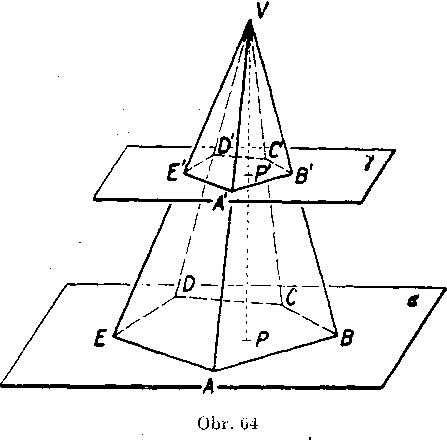
która neprechadza Trchołom F; rovina pretina useóku FPv bodę P'. Ak je p obsah podstawy ihlana a ak p' obsah rezu ihlana rovinou y, plati

p' : p = FP'² : FP².

Strucnejsie móżeme vyslovit vetu takto:

Obsah podstayy ihlana ma sa k obsahu s iiou rovnobeźneho rezu ihlana ako druha mocnina yysky ihlana k druhej moenine yzdialenosti yrcholu ihlana od royiny rezu.

Dókaz (obr. 64, kde sme zvolili pafboky ihlan).

Z.10. roćnika uż vieme, że podstaya ihlana a rez ihlana rovinou y su dva podobne mnohouholniky: móżeme teda poużit vetu 5 o obsahoch podobnych mnohouholmkov. Ak je p obsah podstavy ihlana a p' obsah rezu ihlana royinou y, potom plati

p' : p = k²,

kde k je pomer naśej podobnosti. Ak je totiż P pata yyśky, ktoru sme viedli vrcholom V na rovinu * a P' pata kolmice yedenej vrcholom V na rovinu y, potom pomer podobnosti k je dany yzfahom

k = FP' : VP.

Tento yysledok sme odvodili v 10. rocniku pri preberani ihlana.

Ak dosadime z toho za k do (1), dostavame uż umeru, której plat-nost sme mali dokazat.

Urcime teraz objem ihlana; dokażeme, że plati veta:

Yeta 4. Objem ihlana rovna sa jednej tretine sucinu yelkosti podstayy a yelkosti yysky.

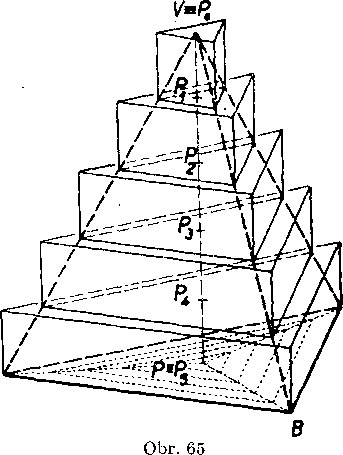
Dokażme to tak, że dany ihlan porovname s dvoma te-lesami stupńoviteho tvaru, których konśtrukciu popiśeme ydalśom.

Nech je dany ihlan s vrcho-lom V a podstayou ABC...

(obr. 65, kde je zobrazeny troj-boky ihlan). Vel’kost jeho vysky nech je v, obsah podstayy ABC. . . nech je p. Oznaćme P patu yysky ihlana, ktoru sme yiedli vrcholom V na rovinu podstayy. Rozdelme vyśku VP / ihlana na n > 1 roynakych casti deliacimi bodmi P₀ = F,

P₂,.. ., P_n = P (na obr. 65 sa n — 5). Każdym z deliacich

bodov (s yynimkou yrcholu F) ved’me rovinu roynobeżnu s royinou podstayy'. Tato royina rozdęli ihlan y mnohouholniku, który je podobny mnohouholniku ABC.. . Uvedenymi rezmi dostaneme ihlany podobne danemu; pre ich yyśky plati

YP_X

v

n ’

VP₀ = 2

n

VP_n = n-

(2)

Ak obsahy podstav tychto ihlanoy postupne oznacime p_y, Pn = potom, ak poużijeme predoslu pomocnu vetu, plati

309