1954 Geometria 350

6% Rotacny valec ma polomer podstayy r, yyśku v, piast p a objem V. Dane je

a)    r = 14,6 cm, v = 23,7 cm,

b)    r = 8,7 cm, p = 23,1 dm²,

c)    t? = 1 dm, V = 1 dm³.

Urcte zvysuju.ce prvky.

7. Urcte polomer rovnostranneho valca, ak noznate jeho piast p. ^yCiselne: p = 300 dm².

(®/Urcte piast, povrch a objem rotacneho yalcaćJŚpypisaneho, b$ opi-’ saneho kocke o hrane a.

9. Obdlżnik o rozmeroch a,b(a > b) możno povażovat dvojakym sposobom za rozvinuty piast rotacneho yalca.

Urcte pomer a) plaśtov, b) povrchov, c) objemov tychto telies.

10.    Piast rotacneho yalca je p, dlźka jeho kruhovej hrany o; urcte objem yalca.

Ciselne: o = 3,7 dm, p = 16 dm².

11.    Dva rotacne valce o polomeroch podstay r_x, r₂ maju rovnake piastę. Urcte pomer ich objemov.

12.    Dva rotacne valce o polomeroch podstay r_v r₂ maju rovnaky objem. Urcte pomer ich plaśtoy.

13.    Dokażte, że piastę a poyrchy dvoch rotacnych valcov, których polomery su v roynakom pomere ako vyśhy, su v rovnakom pomere ako stvorce ich polomeroy alebo yyśok.

14.    Pomer yysky v rotacneho valca k priemeru d jeho podstavy royna sa m : n (m, n su kladne ćisla). Urcte piast yalca, ak viete, że jeho objem je V.

15.    V kotli lokomotiyy zohrieya sa voda horucimi plynmi, które pre-chadzaju 180 rurkami. Każda z nich ma vnutorny priemer 55 mm a dlżku 3,6 m.

Urcte yelkpst yyhreynej płochy v m².

16.    Aky je celkoyy tlak pary ra steny parneho kotła tyaru rotacneho yalca, ak jeho priemer je 1,2 m a dlżka 3,8 m; tlak pary je 8 kg cm^-2.

17.    Kolko kilogramov vażi 15 m dymoyych rur tvarn rotacneho valca s priemerom 40 cm, zhotovenych z plechu, ktoreho 1 m² vażi 7 kg. Pripoćitajte 8% poyrchu na sev.

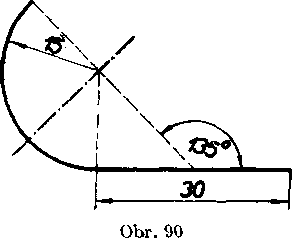
18.    Kolko m² pozinkovaneho plechu treba na zhotoyenie 48 m żlabu daneho prierezu (obr. 90; rozmery su v centimetroch)?

19.    Ako urćime povrch kriżovej klenby, która yznikne z pokmc plas-tov dvoch zhodnych rotaćnych valcov, których osi sa kolmo preti-naju a vzajomne rozpoluju (vyśka valca v je vaćsia neż jeho polomer r).

20.    Poużitim dehnicie 1 z ćl. 1 urcte priamo povrch rotacneho kuzela.

21. Polomer r a yyśka rotacneho kuzela zvacsia sa o kladne eislo s. O kolko sa zyacśi a) piast, b) povrch, c) objem? Ak je e vzhla-dom naras dosf małe, możno ponechat len cleny obsahujuce e v prvej mocnine, a tak vyjadrit pribliżne prirastky.

Urcte ich pre a) piast, b) povrch, c) objem.

Ciselne: r — 5, v = 10, e = 0,001.

22.    Dokażte, że piastę a povrchy podobnych rotacnych kużeIov su v rovnakom pomere ako stvorce polomerov ich podstav alebo vysok.

23.    Rotacny kużel ma polomer podstavy r, vysku v, stranu s, piast p a objem F; urcte ostatne prvky, ak poznate:

a)    r = 10 cm, v = 10 cm,

b) r = 5,8 dm,    s = 12,8 dm,

c) v = 10 cm,    V = 200 cm³,

d) p= 24tt,    V — 12tz.

24.    Dane je a) polomer podstavy r a ostry uhol a strany s podstavou (ciselne: r = 16,5 cm, a, = 65°), b) strana s a ostry uhol * strany s podstavou (ciselne: s = 53 cm, « = 48°).

Urcte piast a povrch rotacneho kuzela.

25.    Urcte pomer a) plaśtov, b) povrchov rovnostranneho kuzela a rov-nostranneho valca (strana kużela s rovna sa strane valca).

26.    Urcte pomer povrchov troch telies, które yzniknu rotaciou pravo-uhleho trojuholnika o stranach a, b, c (kde c je prepona) około jed-notliyych stran,

27.    Urcte povrch rotacneho telesa, które vznikne rotaciou rovnostran-neho trojuholnika o strane a a) około jednej jeho strany, b) około osi idiiccj jednym jeho yrcholom rovnobeżne s protilahlou stranou. Aky je geometricky yyznam podielu poyrchu a obvodu trojuholnika ?

351