1954 Geometria 162

T.Tł Roviny a cf₁ maju priesecnicu p₁; dalej su dane roviny q₂, a₂, o których plati, że q₂ f| a a_% || a_v Dokażte, że roviny o,, a₂ su róznobeżne a że ich priesecnica p_i je rovnobeżna s p_v

14 Dokażte: Existuje jediny par rovnobeżnyeh rovin, z których

V

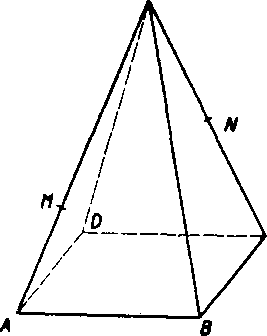
Obr. 21

każda prechadza jednou z dvoch mimobeżnych priamok. i ry. Su dane dve róznobeżne roviny _Q =&C; a s BCD; bod P * D bod na priamke ^4_D. ty) Bodom P ved’te priamku p tak, aby platilo p [ [ q, p 11 a. Zobraz-te pomocou śtvorstena.

B Priamkou p a bodom D je ur-cena rovina r. Zobrazte- jej priesecnicu s rovinami o a a.

16. Zobrazte śtrorsten VABG. Bodom. V ved’te priamky a' || BC, b' |j GA, c'\\AB, Dokażte, że priamky a', b', c' leżia v jednej rovine, która je rovnobeżna s ro-vinou trojuholnika ABC. Popiśte priamky a',b',r.' ako priesecnice urcitych rovin.

17. Je dany pravidelny śtvorboky ihlan (obr. 21), t. j. teleso obmedzene stvorcom ABGD a styrmi zhodnymi rovnoramennymi trojuholnik-mi ADV, BGV, GDV, DAV. Na hrane AV je zostrojeny bod M

tak, że AM — A. V, na hrane GV bod N, który je stredom usec-

O

ky CV. Ved’te bodom N royinu q || MDB a najdite uzayrenu lo-menu ciaru, v której rovina q pretina steny ihlana. Ak su A'B'0'D' yrcholy tej to ciary, dokażte, że body AB-A'B'\ BG.B'C P>C.C’D') DA.D'A' leżia vśetky na priamke p || BD, która je prie-secnicou q a ABC.

5. Polpriestor

Vlastnosfami usporiadania nazyyaju sa v geometrii tie ylasticosti, które sa opieraju o vzfah „bod C leżi medzi bodmi A, B.“ S tymto yzfahom sme sa stretli uż v 7. rocniku; ako najdóleżitejsiu jeho vlast-nost sme vtedy uyiedli tuto zakladnu vetu (axiómu):

Axióma VI. Z troch różnych bodov priamky prave jeden Ml medzi ostatnymi dvoma.

Pomocou yztahu „bod leżi medzi inymi dvoma“ sme v planimetrii definovali dva dóleźite utvary: polpriamku a polrovinu; pripomenieme si ich definicie.

Nech su dane dva różne body P, A; potom polpriamka PA je cast priamky PA skladajuca sa z bodu A a zo yśetkych bodov X priamky PA, które maju tu ylastnost, że medzi A, X neleżi bod P.

Podia tej to definicie prislucha polpriamke PA aj bod P, nazyyany jej zaciatkom.

Nech je dana priamka p a bod A, który na nej neleżi; potom pol-rovina pA je ćasf roviny pA, skladajuca sa z bodu A a zo yśetkych bodov X roviny pA, które maju tu ylastnost, że medzi A, X neleżi nijaky bod priamky p.

Podia tej to definicie. prislucha polrovine pA aj priamka p, nazyyana jej hranicnou priamkou ciże hranicou.

Obdobne zavedieme teraz pojem polpriestoru.

Nech je dana rovina q a bod A, który na nej neleżi. Potom pol-priestorom qA nazyyame cast priestoru skladajucu sa z bodu A a zo yśetkych bodov X, które maju tu ylastnost, że medzi bodmi A, X neleżi nijaky bod royiny q.

Podia tejto definicie prislucha polpriestoru qA aj rovina q (t. j. vsetky jej body). Rovinu nazyyame hranicnou royinou polpriestoru o A. Body polpriestoru qA, które neleżia v rovine q, sa nazyvaju ynutornć. 'Ak je hranicna royina q urcena troma bodmi, napr. q = KLM, zapisujeme polpriestor znakom KLM A (pozor na poradie pismen!).

Polpriestor ma mnoho ylastnosti obdobnych ylastnostiam polpriam-ky a polroviny. Uyedieme bez dókazu najdóleżitejśie z nich.

Rovina q dęli priestor na dva rdzne polpriestory, nazyyane opaSne. Spolocne body obidycch opacnych polpriestoroy yyplnia ich spoloónu hranicnu rovinu q.

Z vyslovenej vety je zrejme, że pri definicii polpriestoru ma hlaynu ulohu rovina q, która uż sama urcuje dvojicu opacnych polpriestoroy, kdeżto bod A iba rozhoduje, o który z oboch polpriestoroy ide; tento bod móże byt nahradeny ktorymkolyek inym ynutornym bodom polpriestoru. Aby sme zdóraznili toto postavenie roviny q, poużivame nazov polpriestor oddeleny royinou q.    .

Priklad 10. Su dane dve rovnobeżne a navzajom różne roviny Q, a. Dokażte, że vśetky body roviny a su ynutornymi bodmi jedneho z polpriestoroy oddelenych royinou q.

163