1954 Geometria 144

spolocny bod, dvoch z tychto priesecnlc boi by totiż spolocnym bodom vśetkych troch rovin, leżał by aj v rovine p_g, aj na priamke p₁₂, taky bod vśak nie je.

Bud je rovina q₃ rovnobeżna s rovinou    potom su g₂, q_s róznobeżne.

To dokażeme takto (obr. 4e): Zvolime bod A na priamke p₁₂, bod B

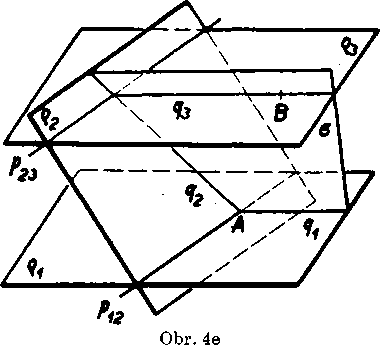
v rovine q₃ a mimo^- rovi-ny o₂. Bodmi A, B polo-żime l’ubovol’nu rovinu a tak, aby neobsahovala priamku p_{l z}. Tato rovina a je zrejme rozdielna od rovin q_±, q₂, q₃, ale s każ-dou z nich ma spolocny bod. Priesećnice roviny a s roninami o_v q₂, q₃ ozna-clme po poriadku q_v q₂, q_s. Priamky q₁, q₃ leżia v tejże rovine a a nemaju spolocny bod; su teda rovnobeżne. Priamka q₂ je róznobeżna s q_v preto-że priamky q₁ aj q₂ pre-chadzaju bodom A; podia vety uvedenej na str. 139 je q₂ róznobeżna aj s priamkou q₃. Ich priesecik je bod spolocny rovinam q₂, q₃\ preto su q₂, q₃ róznobeżne, ako sme chceli dokazaf.

Veta 3. Pre yzajomnu polohu troch różnych rovin marne tychto pat możnosti:

1.    Każde dve z danych rovfn su rovnobeżne.

2.    Dve zdanychrovinsurovnobeźne,tretiajes obidvomaróznobeżna; prisluSne priesecnice su navzajom roynobeżne.

3.    Każde dve z roviri su róznobeżne, ale \setky tri priesecnice su nayzaj om roynobeżne a różne.

4.    frażde dve z danych rovin su róznobeżne, ysethy tri priesecnice splynu y jedinu priamku.

5.    Każde dye z rovin su róznobeżne, każde dve priesecnice su tież róznobeżne. V8etky tri roviny aj ich priesecnice prechadzaju tym istym bodom.

Cvicenie

1.    Udajte, które axiómy sme poużili pri uvahe o existencii dvoch mimo* beżiek.

2.    Aka je vzajomna poloha rovin n a a, ak maju spolocne a) dva body,

b)    tri body, c) priamku a bod, d) dve roynobeżne priamky.

Obr. 5

3.    Udajte obrazy rovnobeżnych, róz-nobeżnych a mimobeżnych pria-mok, róznobeżnych a rovnobeż-nych priamok a rovin (dvojic rovin).

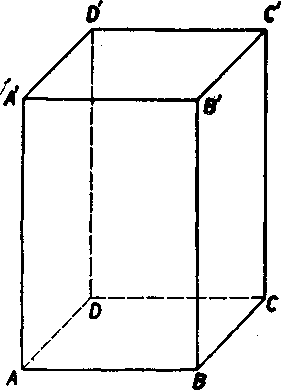
4.    Je dany kvader ABGDA'B'0'D' (obr. 5). Vśetky jeho hrany su na obidve strany predlźene v priamky. a) Udajte vsetky róznobeżky, rovnobeżky a mimobeżky s priam-kou AB a s priamkou CG'. b) Naj-dite tri priamky, z których każde dve su mimobeżky.

5.    Body A, B, C, D neleżia v jednej rovine.

a)    M6żu niektóre tri z nich leżaf na jednej priamke?

b)    Kolko różnych priamok a rovin je tymito bodmi urcene?

c)    Dokażtc, że nijake dve różne z tychto priamok nie su roynobeżky.

d)    Vyslovte a dokażte podobne tvrdenie pre różne roviny.

e)    Najdite vśetky dvojice mimobeżiek.

6.    Nech r a s su dve mimobeżky a p $ ą su dve priamky, z których każda pretina obe mimobeżky r. s. Dokażte, że priamky ^rp, q nie su ani roynobeżne, ani róznobeżne.

7.    Body A, B, C, D neleżia v rovine. Stredy useciek AD, BD, CD su oznacene po poriadku T, U, V. Preskumajte vzajommi polohu troch rovin:

a)    AB U, TUV, BCD:

b)    ABC, BCD, AUV;

c)    ABD, ABC, ABV;

d)    ABC, TUV, BCD.

V ulohe d) dokażte nepriamo, że roviny ABC, TUV su roynobeżne.

145