1954 Geometria 056

Priklad 7 (obr. 69). Bod A leżi zvonku krużnice k. Bodom A pre-ehadzaju dve różne sećny krużnice, a to AKL a AMP (K, L, M, P su body krużnice k). Marne dokazat', żeplati rovnost

AK.AL = AM.AP.

Rieśenie. Uhly <y KLM, -A KPM su obvodove uhly nad menśim oblukom KM. Preto je

A KLM = A KPM .

Trojuholniky AKP a AML maju spolocny uhol pri vrchole A a zho-duju sa v uhloch <1 ALM, <j; APK. Preto je podia vety uu

Z toho vyplyva

cize

A ALM ~ A APK.

' AL _ AM AP ~ AK’

AK.AL = AM.AP.

Priklad 8. A ABC je pravouhly trojuholnik; jeho ostre uhly su 30°, 60°. Mamę dokazat, że vel’kosti jeho stran su v pomere 1 : |/3 : 2 (obr. 70).

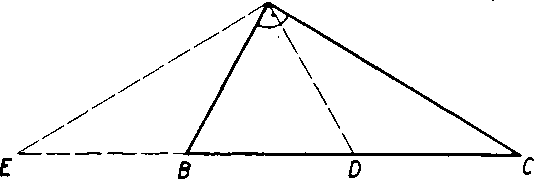
Obr. 70

Rieśenie. Oznaćenie vol’me tak, aby boi A = 90°, <£ B = 60°, <£ O = 30°. Medzi bodmi B, C zostrojme bod D tak, aby platilo A BAD — 60°, Ą GAD = 30°. Takto vznikne rovnostra,nny trojuholnik ABD (pri yrcholoch A, B ma uhly ve!kosti 60°) arovno-ramenny trojuholnik ACD (pri vrcholoch A, C ma uhly veIkosti 30°). Preto je

(6)    AB — BD = CD.

Dalej nanesieme usecku AB na polpriamku opacnu k BC; dostaneme bod E a zostrojime A A BE. Trojuholnik ABE je rovnoramenny (AB = BE) a jeho uhly pri zakladni AE maju veIkos£ 30°, pretoże A ABE = 120°. Podia vety uu je

AACD~ AECA.

Z toho vyplyva rovnost

AC CE

~CD ~~ AC

(⁷)

Ak zvolime usećku AB za jednotkovu, je podia (6) CD = 1 a CE = = EB -f BD -f- DC = 3. Zo vztahu (7) potom vyplvva

ciże

AC =

3

AC

AC = ]/3.

Pretoże BC = BD + DC = 2, je

AB : AC : BC = 1 : |/3 : 2.

Cvicenie

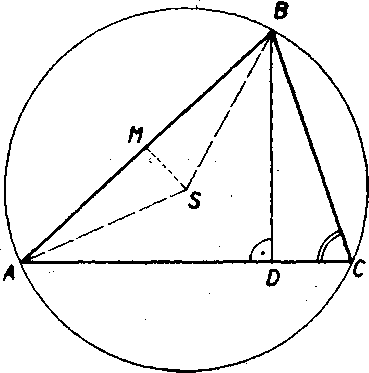
Obr. 71

1.

2

Dva roYnoramenne trojuholniky, które sa zhoduju v uhloch opro-ti zakladniam, su podobne. Dokażte to.

Marne styri trojuholniky ABC, FGH, A&O^ DTE. O ich uhloch plati

(1) y ,1 .40 ,

= 80°,    <7 = ?; (2)

F = go°; a o = '72°, A H = ?; (3) 3 A = 60°, < A =

= j < Bi, (4) -A D =

= 72°, AT = -1 AD, AE = *■

Bozhodnite, które dva z tychto trojuholnikov su podobne.

57