1954 Geometria 060

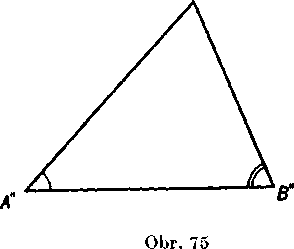
Dókaz (obr. 73). K dvom danym trojuhołnikom ABC, A'B'C' zostrojime este pomocny trojuholnik A"B"C" tak, aby platilo

(1)    A"B" = A'B', A" = A, <£ B" = ■£ B.

Podia vety o sućte uhłov trojuholiuka je potom aj

(2)    <£ O" = <£ C.

Okrem toho je vsak podia vety uu A ABC ^ a A"B"C". Pretoże podia predpokladu je A ABC ~ A A'B'C', z vet,y 1 vyplyva, żc A A“B”C” ~ A A'B’C'. Pomer tejto podobnosti rovna sa jednej, pretoże płat! A'BT = A'B'. Trojuholniky AT WG" a A'B'C' su teda podia vety sss zhodne a plati

(3)    <£ A"=* <£ A\ < B"= <£ B',    <?" = < C'.

Spojenim vz€ahov (1), (2), (3) dostaneme vzfahy

A = < d',    < C =    (?',

które sme mali dokazaf.

.4

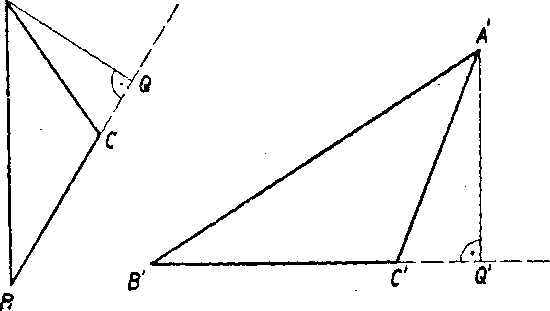
Obr. 74

Priklad 9 (obr. 74). Nech su ABC, A’B’C’ dva podobne trojuholniky, pre które plati

A’B’ = Z-.dB, £'C' =    CA’ = ft.CM.

Potom pro vySky AQ, A'Q', które su prlslusnó sfcranam BO a B'C, plati

A’Q' = k.AQ.

Dokaźte.

Dókaz tvrdenia: Podia vety 3 je ABC — <C A'B'C'. Ak je Q ~ B, je <£ .4BC pravy; preto je aj <£ A’B'C pravy, t. j. s B'. Yztah A’Q' = k.,4Q je potom totożny so vz£ahom A'B' --- k.AB.

Ak je Q $ B, je aj Q' $ B’ a vzniknu dva pravouhle trojuholniky ABQ, A'B'Q'. Podia vety uu je

plati teda

eo sme mali dokazaf .

A ABQ ~ A A'B'Q'\

A'Q' _ A'B'_

AQ ~ AB ~^k’

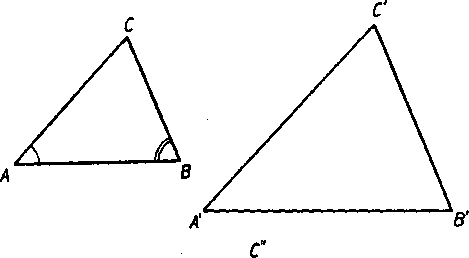
Podobnosf trojuholnlkov vieme doteraz zistit’ bud’ podia definlcie, bud’ podia vety uu. Teraz odvodlme dalśiu vetu o podobnosti trojuhol-nlkov, która je obdobnou vetou vety sus o zhodnosti trojuholnlkov.

61