1954 Geometria 214

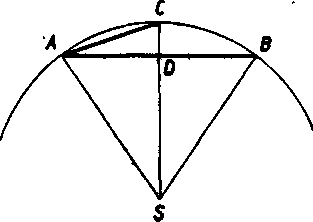
Navod. Poużite Pytagorovu vetu na trojuholniky Ą ACD, A AD8 (obr. 68) a podmienku DS -f- CD — r.

Aka je yelkost vnutorneho uhla pravidelneho n-uholnika pre n = = 3,^5,6^)8010?

2. Hranolovy priestor, hranolov& płocha, hranol

Doteraz sme sa velmi mało zaoberali telesami, które su v priestore obdobou rovinnych obrazcov. Prileżitostne sme hovorili o kvadri,

o kocke, o śtvorstene, o niektórych hranoloch a ihlanoch. Ich existeń-ciu sme vaćśinou prijimali z nazoru a len na niekolkych ukazkach sme ju presne dokazovali, a to dosf zlo-źite. Teraz si zavedieme jednoduche zakladne telesa presne.

Obr. 68.

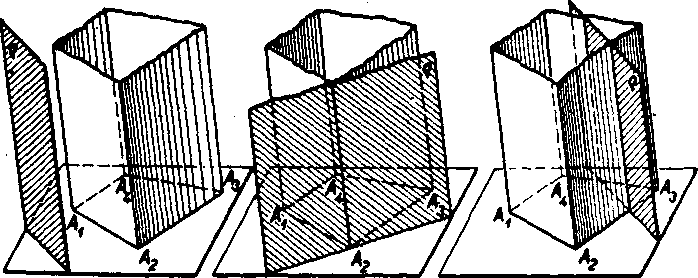
Definicia (obr. 69). Je dany vy-pukly mnohouholnik A_x A₂.... A_n, który leżi v rovine q, a dalej smer p róznobeżny s q. Mnożina priamok smeru p, ktoró pretinaju q v bodoch mnohouholnika, vypliiuje hranolovy priestor.

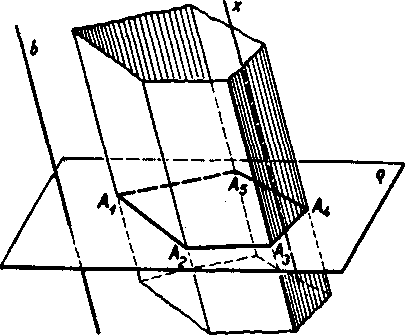
Mnohouholnik A_XA₂.... A_n z pre-doślej definicie budeme nazyvat ria-diacim mnohouholnikom hranoloveho priestoru.

Priamky hranoloveho priestoru, które pretinaju obvod riadiaceho mnohouholnika, vyplńaju tzv. hranolovu płochu. Ostat-ne priamky hranoloveho priestoru su vnutornymi priamkami hranoloveho priestoru a vyplńaju vnu-tro hranoloveho priestoru. Ich body su vnutor-nymi bodmi hranolovóho priestoru. Hranolovy prie-Obr. 69.    stor sa teda składa z vnń-tra a z hranoloyej płochy a tieto dva iitvary nemaju nijake spo-locne body.

Priamky hranolovej płochy, które prechadzaju vrcholmi riadiaceho mnohouholnika, nazyraju sa boCne hrany. Każda hranolova płocha

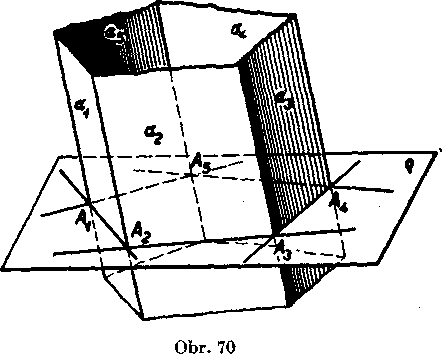
ma konecny poćet hran, a to aspoh tri. Ak je tento pocet n, vola sa hranolova płocha n-boka a aj hranolovy priestor je w-boky. Hrany, które prechadzaju dyoma susednymi yrcholmi riadiaceho mnohouholnika, su susednś hrany. Priamky hranoloyej płochy, które pretinaju

a)

b)

Obr. 71

c>

215