1954 Geometria 098

1.    Ak zostrojime pravouhly trojuholnik, ktoreho useky na prepone budu mat vel’kos£ x, y, budę mat podia Euklidovej vety o vy§ke vyska veIkost z. Zostrojenie (pomocou Taletovej vety) znazorhuje obr. 112.

2.    Ak zostrojime pravouhly trojuholnik, ktoreho prepona budę mat vel’kost y a jeden usek prepony veIkosf x, prilahla odvesńa budę mat veIkos£ z. Zostrojenie (opat pomocou Taletovej vety) znazorhuje obr. 113.

Viete, że pravouhly trojuholnik je urceny dvoma stranami, a to bud dvoma odvesnami podia vety sus, bud odvesnou a preponou podia vety Ssu. VeIkost tretej strany możno teda vypocitat z vel’kosti dvoch stran. Jeden spósob vypoctu uż pozname: Poużili sme goniometricke funkcie (pr. 17 cl. IV/5). Iny spósob vyplyva zo vztahu, który plati medzi stranami pravouhleho trojuholnika a który sa vola veta Pyta-gorova.

Veta 2. (Veta Pytagorova.) Ak je a yelkosf prepony pravouhleho trojuholnika, b, c velkosti jeho odvesien, je

a² = ó² + c².

Inac vyslovujeme vetu Pytagorovu takto:

Obsah śtvorca zostrojeneho nad preponou pravouhleho trojuholnika rovna sa suctu obsahov obidvoch śtvorcov zostrojenych nad jeho od-vesnami.

Dókaz. Ak poużijeme oznacenia z vety 1 (obr. 111), je podia Euklidovej vety o odvesne

ó² — a.b_v c² = ac_v

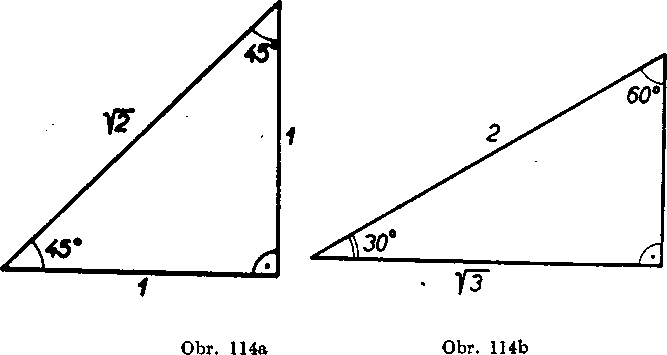
b² -f c² = a(6_x + c_x) = a. a = a², pretoże pata vysky £) leżi medzi vrcholmi B, C.

Poznamka. S osobitnymi pripadmi Pytagorovej vety sme sa uż stretli pri pravouhlom trojuholniku rovnoramennom (pr. 8) a pri pravouhlom trojuholniku, który mai uhly 30°, 60° (pr. 8). Tam sme zistili, że v prvom pripade (obr. 114a) je pomer stran 1 :1 :]/2, v druhom pripade (obr. 114b) 1 : ]/3 : 2. Ak oznacime vel’kost najkratśej odvesny x, su vel’kosti stran pravouhleho trojuholnika rovnoramenne-ho x,x,x^2, skutocne teda plati

x² -f x² = (x]/2)².

U druheho pravouhleho trojuholnika su potom vel’kosti stran x, a;]/3, 2x, plati teda aj

z² + (z]/3)² = (2x)².

Priklad 2. Ak je ABC tupouhly trojuholnik s tupym uhlom pri yrchole A, pre vel’kosf jeho stran plati vztah

BC² > AB² + AC².

⁽¹⁾

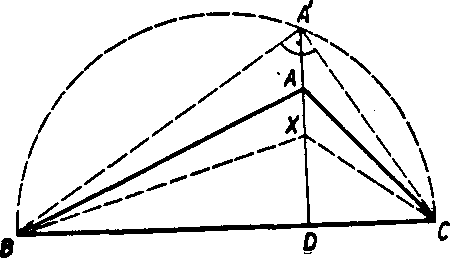
Dokażte to. Rieśenie. (Obr. 115.) Pata D vyśky AD leżi medzi bod-mi B, C. Na pol-priamke DA zostrojime bod A' tak, aby <£ BA 'C boi pravy. Toto je możnć podia vety Taletovej (obr. 115).

Bod A' neleżi medzi bodmi A, D.

Pretoże pre każdy    _{0br 115}

bod X leżiaci medzi

bodmi A, D plati podia vety o vonkajśom uhle trojuholnika ^BXD > <BAD, <£CXD > <ŹCAD, teda po sćitani obidvoeh vztahov

$.BXC > ^BAC.

99