1954 Geometria 046

zvolime stranu śtyorca za jednotkoYU usecku a ak oznacime u veTkos£ uhlopriecky, dostaneme ako v uvedenom prikladc

u² = 2.

Z toho vyplyva u = ]/¥; hladany pomer je teda J/2 : 1.

Cv.ieenie

1.    Morska mila ma vel’kos(’ 1 855 m. Oznacte x vel'kośt usecky v km, y v morskych milach. Yyjadrite y pomocou x.

2.    Aku Yelkosi ma strana śtvorca, ak zvolime za jednotkovu usecku dve tretiny jeho uhlopriecky?

c

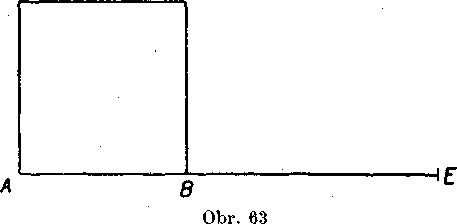
3. Na obr. 63 je śtvorec AB(J1): AB = 2, BE = 3. Yypocitajte vzdia-lenost bodu E od priamky AC. Navod: Vypocitajte obsah trojuhol-nika AEC.

4.    Rozdelte danu usecku v pomerc ]/ 2 : j/^3.

5.    Na predfżeni usecky AB za bod B mamę zostrojif bod X tak, aby

AX

BX

platilo

= lc, kde k je cislo vaćśie neż 1. Móżeme postupovai

takto: Na polpriamku AB nanesieme usecku veIkosti —^AB

a vyslednu iisecku rozdelimc v pomere k : 1; tak dostaneme bod X. Dokaźte to.

6.    iJsecku dlźky 12 cm rozdelte na 3 ńsecky tak, aby ich ve!kosti

boli v pomere 1 : ]/ 3 : 2.

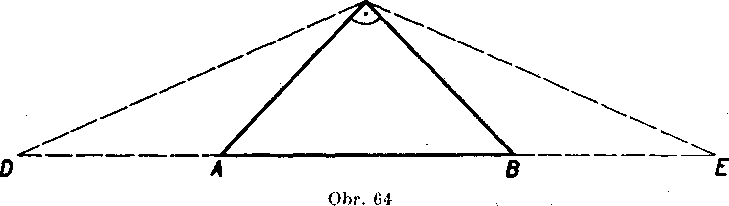
7.    Useeka dlźky 14 cm je zhodna s obvodom pravouhleho rovnoramen-neho trojuholnika. Urćte jeho strany vypoctom i konśtrukóne. Navod (obr. 64): Ak je ABC hladany trojuholnik, zostrojte rovno-ramenny trojuholnik CDE, lcdc AD = AG — BC = BE.

47