1954 Geometria 146

8. Obr. 6. Steny v cel ej bunky budeme povażova£ za casti rovin. Ak pozorujete niekolko susednych buniek v charakteristickom zoskupeni, v akom su v ule, móżete yybrat z rozśirenych stien tro-jice rovin, które maju vśetkych pafi vzajomnych polóh. Ocislujte steny a zapiśte.

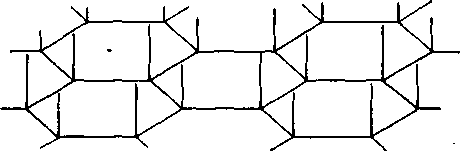
Obr. 6

3. Konstrukcne uloliy y priestore

V planimetrii ste riesili vel'mi mnoho konśtrukcnych uloh. Cielom konśtrukćnej ulohy bolo narysovat utvar vyhovujuci urcitym podmienkam (napr. stred krużnice vpisanej do trojuholnika, alebo krużnicu o danom polomere, dotykajucu sa danej priamky a krużnice, alebotrojuholnik s danymi fażnicami a pod.). V stereometrii je to zlo-żitejsie. PriestoroYÓ ulohy nemożno narysovat, bolo by ich treba mode-lovat. Aj taku ulohu, ako je napr. urciti priecku dvoch mimobeżiek prechadzajucu danym bodom, bolo by treba riesit modelovanim. Kedze vśak modelovanie je technicky obtażne, ba niekedy nemożne a nedava presne vysledky, konstrukcnu ulohy v stereometrii rieśi-me inak. Spravidla poużivame jeden z tychto spósobov:

A.    Bud’ zobrazime urcitym vopred dohovorenym sposobom prie-storovy utyar v rovine (v nakresni) a konstrukcnu ulohu rieśime v tom to obrazę.

B.    Bud’ ulohu rieśime tym, że postupne urobime niekolko rovinnych konśtrukcii v różnych rovinach. Vśetky rovinne konstrukcie rysujeme vedl’a seba v nakresni, t. j. napr. na listę papiera, na ktorom rysujeme.

A. K prvemu sposobu riesenia konStrukćnych uloh. Priestorove utvary, najma telesa a ich casti, zobrazujeme zyycajne sposobom, który nazyyame vol’nym rovnobeżnym premietanim (yolnou rovno-beżnou projekciou). Słovo ,,rovnobeżne“ niekedy yynechayame.

Yol’ne rovnobeźne premietanie je zobrazenie, które sa opiera o tieto dohovory:

(a)    Rovinne obrazce leżiace v roninach roynobeżnych s nakreshoU zobrazuju sa v skutocnej ve!kosti a v skutocnom tvare.

(b)    Dve rovnobeżne priamky sa zobrazuju alebo ako dva body, alebo ako dve rovnobeżky.

(c)    Dve rovnobeżne a zhodne usecky sa zobrazuju alebo ako dva body, alebo ako dve rovnobeżne a zhodne usecky.

(d)    Ak je obrazom usecky AB usecka A'B' a ak leź! bod G vnutri usecky AB, potom jeho obraz C' leż! vnutri usecky A'B' a piat!

A'G’ _ AG B'C' ~ BC'

Poznamky. Z dohovorov (a), (b), (c), (d) nevyplyva, że napr. każde dve zhodne usecky zobrazujii sa ako dve zhodne usecky. Ani usecka a jej obraz nemusia byt vżdy zhodne. Ani kolme priamky sa nezobrazuju vżdy ako kolme priamky. Vśimajte si irmlene vlastnosti vo vśetkych prikladoch, które budeme rieśit.

Kvóli jednoduchosti budeme znacit bod, priamku, usecku a pod. v priestore aj ich obrazy vo vol’nej projekcii tym istym pismenom.

Priklad 2. Je dany kyader ABCDA'B’G'D' v tzv. zakladnej polohe;. t. j. steny ABB'A' a DGCD’ su rornobeżne s nakresnou. Rozmery kvadra su AB — 4 cm, AA' — 9 cm, AD = 6 cm. Bod P je stredom usecky B’C, bod Q leżi na priamke A'B' tak, że A' je stre-dom usecky B'Q. Marne zobrazit vo vol’nej projekcii dany kvader a jeho priesek s rovinou BPQ.

Riesenie (obr. 7). Narysujeme obdlźnik ABB'A' a danymi roz-mermi [vlastnost (a)]. Bodom A vedieme IubovoInu priamku m róznu od AB a AAZvolime na nej bod D ako obraz prisluśneho bodu priestoru. Spravidla volime priamku m tak, aby platilo <^C DAB — == 45° a aby yelkosfi usecky AD bola pokmca daneho rozmeru (v na-som pripade 3 cm). Potom zostrojime body G, C’, D’ tak, aby bolo BG || B'C || A'D' || AD a BO = B'C = A'D' = AD [vlastnost (c)]. Narysujeme obrazy ysetkych 12 hran kvadra; pritom ciarkujeme tie, które boli pri pohlade zhora sprava na nepriehladne teleso neviditel’ne (v naśom pripade AD, CD, DD').

Obraz P prisluśneho bodu P v priestore je podia yłastnosti (d) stredom usecky B'C'. Obdobne zostrojime bod Q.

Roriny A'B'C', BPQ, ADD' sa pretinaju vjedinom bodę R, który lezi na priesecnici każdych dvoch z nich. Priesećnica rovin BPQ,

147