1954 Geometria 282

Ob sali menśieho odseku prisluchajuceho k tetive AB (obr. 35) uroi-me ta k, że ho doplnime trojuholnikom /\ASB na vysek, ktoreho uhol je du 1y uhol ASB.

0 bsah vacśieho odseku prisluchajuceho k tetive AB (obr. 36) urci-me tak, że ho rozlożime na trojuholnik A ASB a vysek, ktoreho uhol je \ypukly uhol «£ ASB.

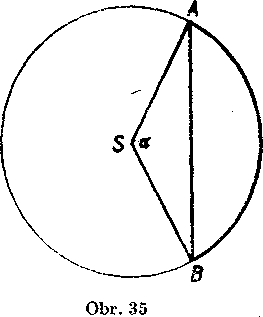
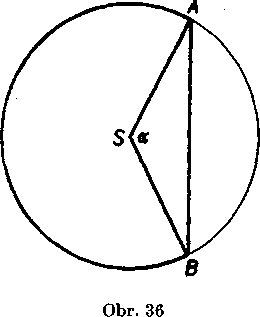
Obsah trojuholmka /\ASB urćime trigonometricky. Ak duty uhol ^ASB oznaeime a, obsah trojuholnika ASB je dany znamym vzorcom

^PA — J ^r*^sin*-

Uhol cc urćime pomocou tabuliek z rovnice

l _

a

2r'-

sm

2 r

kde a je Telkosf tetivy AB (obr. 35, 36).

Obsah n tnsieho odseku prisluchajuceho k tetive AB

T> ^nrZ%    1    2    •

^P= 360 - T

Obsa h yaeeieho odseku prisluchajuceho k tetive AB je

nr²(4R—a) 360

— r² sin*. 2

Poznamka. Ak je uhol <^ASB mały, możno obsah odseku prisluchajuceho k tetive AB (obr. 37) vyjadrif pribliżne zo vzorca

2

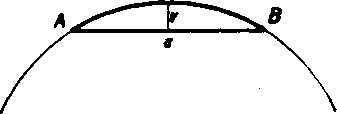
Obr. 37

Możno dokazaf, że ked' uhol <£ ASB je menśi neż 5°, rozdiel medzi skutocnou a vypocitanou hod-notou je menśi neż jedno per-cento obsahu.

Presnejśie yysledky posky-tuje zlożitejśi vzorec

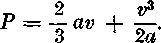
Cvicenie

1.    Odvod’te vzorec pre obsah medzikrużia urceneho krużnicami o po-lomeroch r_x < r₂ [P = n{r\ — rf)].

2,    Odvodte vzoreo pre obsah yyseku medzikrużia (obr. 28).

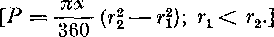
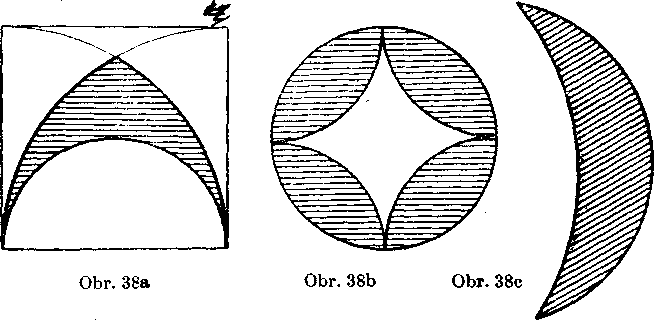
3.    Ukażte, że utvary na obr. 38 su obrazce.

4.    Urcte obsah odseku prisluchajuceho tetive AB, ak je dany uhol a = <£ ASB apolomer kruhu. (Rozliśujte tri pripady: a) 0 < « <

<    2B, b) a = 2B, c) 2B < a < 4B.)

5.    Urcte obsah odseku prisluchajuceho k tetive AB, ak je dana vzdia-^ lenost d < r tejto tetivy od stredu kruhu. ZvoIte si r — 5, d — 2. 6) Urcte obsah obrazca na obr. 39 (polomer kruhu je r; 0 < a < b <

<    r). Zyolte si r = 5 cm, b = 4, a = 2,5.

283