1954 Geometria 032

II. YEEKOSl’ TJSECKY 1. Pojem yelkosti useeky

Jeden z prvych geometrickych pojmov, s którym ste sa oboznamili u ż na narodnej śkole, je yefkosf ciże dlzka useeky. Yelkost useeky je cislo a urcujeme ju meranim.

Ak mamę zmerat usecku AB (obr. 50), zyolime urcitu usecku CD za jednotkovu (t. j. priradime jej cislo 1) a zostrojujeme na polpriamke AB navzajom różne body P_1; P₂, P₃,... tak, aby platilo

APi = P_XP₂ = P₂P₃= ... = CD;

strucne povieine, że usecku CD nanaśame postupne na polpriamku AB. Ak niektóry z bodoy P_lt P₂,... spłynie s bodom B, ciże ak pre niektóre n je P_n ~ B (napr. pre n -- 5 na obr. 50), je ve!kost useeky AB prirodzene cislo n.

A    B A    B

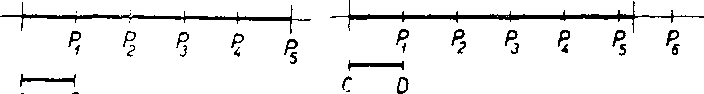
Obr. 50    Obr. 51

Obycajne vśak nastanę pripad znazorneny na obr. 51. Tu leżi bod B medzi bodmi Pn’ Pn+1 (n == 5); meranim sme teda nezistili vel’kost useeky AB. V tomto pripade su dve możnosti;

]. Jednotkovu usecku GD możno rozdelit na urcity poóet zhodnych diełov, napr. na q dielov tak, że ak zvolime jeden z tychto dielov za novu jednotkovu usecku, je vel’kost useeky AB prirodzene cislo p. (Na obr. 51 je q = 3, p = 16.) V tomto pripade sa yelkosf useeky AB

pri jednotkovej usecke GD rovna racionalnemu cislu — (na obr. 51 je yelkost ~).

2. Może sa vśak stat, że usecku CD nemożno rozdelit nijakym sposobom na zhodne diely tak, aby nastał pripad 1. To znamena, że yelkost useeky AB pri jednotkovej usecke GD nemożno yyjadrit nijakym racionalnym cisi om (a teda ani celym cislom). Potom hovorime, że usecka AB je nezmeratelna useckou CD. Nezmeratelne useeky sku-tocne existuju, ako nam to znazorńuje nasledujńci priklad.

D    C

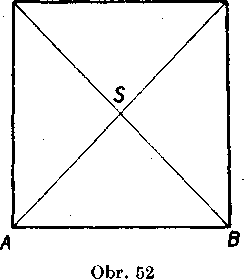
Priklad 1. Mamę dokazat, że uhlo-priecka śtyorca je nezmeratelna jeho stranou.

Rieśenie. Toto tvrdenie dokażeme nepriamo. Na obr. 52 je śtvorec ABGD, jelio uhlopriecky AC, BD ą ich prie-seeik 8. Stranu śtyorca zyolime za jednotkoYU usecku; budę mat teda yelkost rovnu jednej. Predpokladajine teraz, że vel’kost uhlopriecky AC je ra-cionalne cislo u. Uhlopriecky delia śtvo-rec na śtyri zhodne trojuholniky ABS, BCS, CD8 a DA8; każdy z nich ma dve odvesny, których yelkost je racio-

U

nalne cislo —. Obsah każdeho z tychto śtyroeh trojuholnikoy, ako

Li

33