1954 Geometria 186

3. Yzdialenosf bodov, priamok a royin

V planimetrii sme s pojmom kolmic spajali pojem vzdialenosti bodu od priamky. Aj v stereometrii budeme definovaf tento pojem.

Definicia. Nech je dana priamka p a bod A. Ak leźi bod A na priamke p, jeho yzdialenosf cd priamky rovna sa nule. Ak neleżi bod A na priamke p, jeho yzdialenosf od priamky rovna sa vzdialenosti bodu A od priamky p urćenej v rovine Ap.

Aj z planimetrie je dobre zname — a prenaśa sa to bezo zmeny do stereometrie — że yzdialenosf bodu A od priamky je najmensia zo y.śetkych yzdialenosti bodu A od jednotliyych bodov priamky. Dokaż si 1’ahko urobi te v cyićeni.

Celkom obdobnu definiciu a obdobne ylastnosti ma aj yzdialenosf bodu od roviny.

Definicia. Nechjeda-na rovina o a bod A. Ak leżi bod A v rovine o, jeho yzdialenosf od roviny rovna sa nule. Ak bod A neleżi v rovine g, jeho yzdialenosf od roviny g royna sa yzdialenosti bodu A od paty kolmice y e-denej kroyine gbodom A.

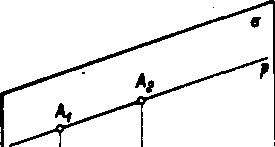
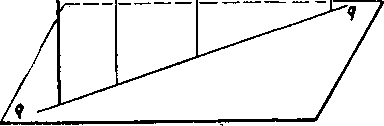
^0br- 41    ny; to si opaf dokażeme

v cvićeni.

Pomocou pojmu yzdialenosti bodu od roviny możno vyslovif nove kriterium rovnobeźnosti priamky a roviny, które je niekedy pohodl-nejśie neż prvsie kriterium (veta 6).

Yeta 24. Ak możno na priamke najsf dya rdzne body A_1} A_a, leżiaee yfomistompolpriestore, oddelenom royinou g. których yzdialenosti od roviny p su rovnake, potom je priamka p rovnobeżna s rovinou g. (Obr. 41.)

Dokaż. Nech su body A_t a A₂ na priamke p najdene tak, że yyho-vuju predpokladom yety. Ved’me nimi kolmice na rovinu o a polożme tymito kolmicami rovinu a. Priesecnica o. a prechadza obidvoma pa-ći86 tami kolmic a podia znamy oh ylastnosti z planimetrie je rovnobeżna s priamkou p. Potom je vsak p \ \ o podia predosleho kriteria (veta 6).

Obdobnym postupom ako v dokaże vety 24 możno zistit, że każdy bod priamky p rovnobeżnej s rovinou q ma od roviny q tu istu yzdialenosf.

Uvedena poznamka nam dovol'uje definovat yzdialenosf priamky od roviny s ńou rovnobeżnej ako vzdialenost jej Iubovol’ne-ho bodu od tejto roviny.

Aj o dvoch rovnobeżnych rovinach możno vyslovif po-dobnu vetu, która może slużif ako nove kriterium rovnobeż-nosti dvoch rovin.

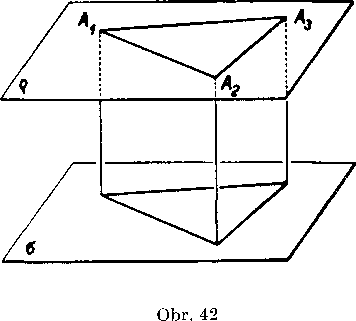
Veta 25. Ak możno v rovine q najsf tri body A_v A₂, A_s, które neleżia na jednej priamke, leżia vsak vsetky v tom istom polpriestore oddelenomrovinou a a ich yzdialenosti od tejto ro-viny su rovnake; potom su ro-yiny pac roynobeżne.

Dókaz. (Obr. 42.) Neeh body A_v A₂, A_s, su take body roviny g, które vyhovUju predpokladom vety. Potom su obidve róznobeżne priamky A₁A₂, A_XA₂ roynobeżne s rovinou a, co vyplyva z predcha-dzajucej yety 24. To vsak znamena, podia prysieho kriteria rovno-beżnosti dyoch rovin, że q || a.

Obdobnym sposobom ako v dokaże vety 25 aj tu możno zistit, że każdy bod roviny a roynobeżnej s rovinou q ma od roviny q tu istu yzdialenosf.

Tato poznamka nam opaf umożhuje zaviesf novy pojem, a to pojem yzdialenosti dyoch rovnobeżnych rovin. Yzdialenosf dvoch rovno-beżnych rovin je yzdialenosf 1’uboyolneho bodu jednej royiny od drp-hej roviny.    «

Priklad 6. Dokażte, że existuje teleso, obmedzene śiestimi ob-dlźnikmi (kyader).

Riesenie (obr. 43). Neeh je ABCD obdlżnik s IubovoTnymi roz-mermi. V bodoch A, B, 'C, D ved’me kolmice na royinu ABCD, Tieto kolmice su nayzajom roynobeżne. Na każdej kolmici urcime body, a to po poriadku body A', B’, 6". ])', yśetky v tom istom polpriestore,

187.