1954 Geometria 006

2.    Obn 8. Dokażte, że sa usećky AB, CD pretinaju (t. j. maju spolocny bod, który nie je krajny).

3.    Je dana priamka PQBS. Vyznacte polpriamky a) opaćne, b) które nemaju spolocny bod, c) których spolocnou casfou je niektóra useć-ka, d) których spolocnou casfou je niektóra polpriamka.

4.    ABCD je śtvorec, S je priesecik jeho uhlopriecok. Urcte spolocnu ćasf a) polrovin CDS, ASB, b) polroviny ADB a duteho uhla <£ ASD, c) uhlov ASB a <r. BDC.

°2

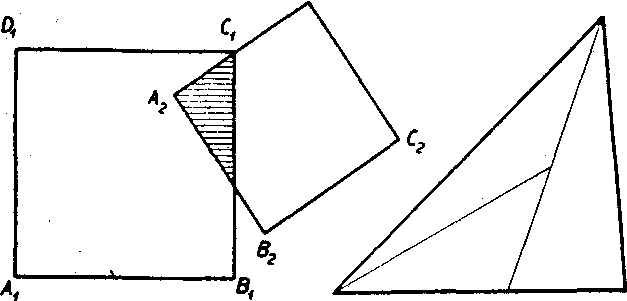
Obr. 9    Obr. 10

5.    Dva śtvorce ^₁5₁(7₁Z)₁ a A₂B₂C₂D₂ majupolohu podia obr. 9.Vyznacte spolocnu casf obidvoch śtvorcov pomocou polrovin, urcenych ich yrcholmi.

6.    Na obr. 10 je pat trojuholnikov. Oznacte ich vrćhoły a yyznacte pre każdy z trojuholnikov vśetky vonkajśie uhly, które su vnutorne pre iny z tychto piatich trojuholnikov.

2. Zhodnosf uscgiek a uhlov

Jeden z hlavnych geometrickych pojmov, s którym ste sa obozna-mili, je pojem zhodnosti. Predstavujeme si, że zhodne su dva rovinne utvary, ktoró możno na seba polożit tak, że sa kryju. Podia tejto pred-stavy su zhodne każdd dve priamky, kaźdó dve polpriamky, każde dve połroviny; aj rovina je zhodna sama so sebou; nie su vśak zhodne każde dve usećky, każde dva uhly alebo każde dva trojuholniky. Preto ste nehovorili o zhodnosti priamok, polpriamok, polrovin, ale zaoberali ste sa iba zhodnosfou usećiek, uhlov a trojuholnikov.

Najdóleżitejsia poućka o    B

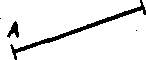
zhodnosti usećiek je tato:

(4) Danu usećku AB możno premiestif s jedinym vy-sledkom na darni polpriamkn PQ tak, aby bod A preSiel

do bodu P a bod B do urći- b-¹    I--+--

teho bodu 8 polpriamky PQ P    S    «

(obr. 11). Inać povedanć: K

danej usećke AB możno zo-    Qk_r i [

strój it na danej polpriamke PQ jedinu usećku PS, zhodnu s AB.

Zostrojenie usećky PS sa obyćajne nazyva prenesenim usećky AB na polpriamku PQ. Prenaśanie usećiek nam umożńuje usećky porovnavaf, graficky sćitat a odćitat.

O zhodnost usećiek sa opiera pojem stredu usećky. Stred usećky AB je taky bod S priamky AB, pre który su usećky 4$, BS zhodne, t. j. pre który plati AS — BS. Je zname, że każda usećka ma jediny stred.

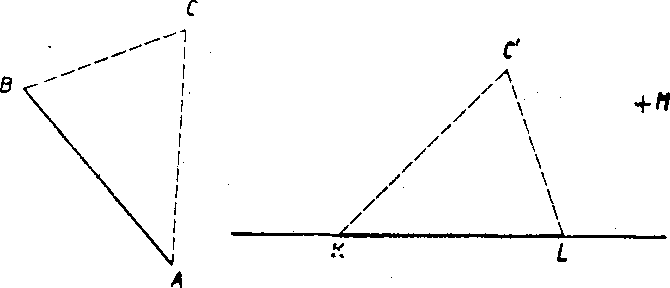
Obr. 12

O zhodnosti rovinnych utvarov, które nie su ćastou priamky, plati tato zakladna veta znama zo ,7. roćnika:

(5) (Obr. 12.) Nech su danć v rovinnom iitvare tri body A, B, 0, które neleżia v priamke; v rovine tohto utvaru ncch je dalej dana usećka KL =

7