1954 Geometria 208

obvodu mnohouholnika leżia vo vnutri obidvoch polrovin oddelenych priamkou QE (pozri body H, L). To je vśak y rozporę s ylastnostou 3. definicie mnohouholnika.

Definovali sme yypukly mnohouholnik ako utvar zlożeny z troj-uholnikov A OA_xA₂, A OA₂A₃,..., A OA_n-_xA_n, A OA_nA_x (obr. 57, kde n = 6). Nech su pre takto definovany n-uholnik splnene eśte dalsie dve podmienky:

a

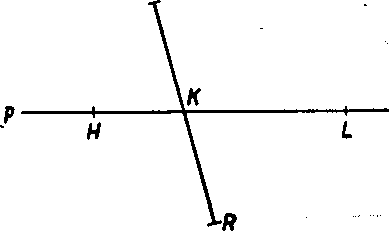
Obr. 60

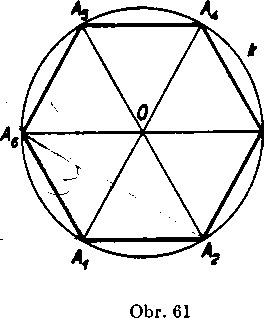
4.    Vrcholy A_v A₂, A₃, A leżia na krużnici k, której stredom je bod O.

5.    Vśetky uhly <£ A₁OA₂, <£A₂OA₃,....., <£ A_nOA_v su navzajom

zhodne (obr. 61).

Definicia. Mnohouholnik, który spina podmienky 1 aż 5, nazyva-me pravidelnym mnohouholnikom.

Pretoże pravidelny mnohouholnik je len osobitnym pripadom vy-pukleho mnohouholnika, plati o nom vśetko to, co sme povedali o vy-puklom mnohouholniku.

Trojuholniky A OA₁A₂, A OA₂A₃, A OA_nA₁ su rovnoramenne (pretoże OA₁ = OA₂ ... = OA_n) a zhodne podia vety sus (z podmienky 5 totiż vyplyva, że sa tieto trojuholniky żhoduju v uhloch pri

4i?

yrchole O; każdy ztychtouhloy ma yelkosf —-). Zo zhodnosti uvede-nych trojuholnikov vyplyva, że

A}A₂ = A₂A₃ = ....== A_n-₁A_n = A_nA_1}

t. j., że vśetky strany prayidelneho w-uholnika su navzajom zhodne;

A_XA₂A₃ ⁼    -^2-^3-^i ⁼ ■ ■ ■ — -dn.-i A_nAi = A_nA_xA₂,

t. j., że vsetky ynutorne uhly prayidelneho w-uholnika su nayzajom zhodne.

Pretoże sućet yelkosti ynutornych uhlov yypukleho w-uholnika rov-na sa 2R (n — 2), vel'kost każdeho vnutorneho uhla prayidelneho n-uholnika rovna sa

2R (n — 2) n

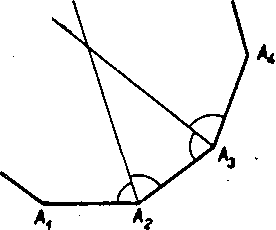
Obr. 62

Krużnica k, na której leżia vrcholy prayidelneho w-uholnika, vola sa opisanou kruźnicou tomuto n-uholniku. Z definicie prayidelneho M-uholnika bczpro tredne vyjjlyva, że każdemu prayidelnemu w-uhol-niku możno opisat krużnicu, t. j. możno zostrojif krużnicu, która pre-chadza yśetkymi jeho yrcholmi.

V naukę o trojuholnikoch ste do-kazali, że każdemu trojuholniku możno ypisaf krużnicu, t. j. możno zostrojit krużnicu, która sa dotyka yśetkych troch stran tohto trojuhol-nika. Podobne krużnicu dotykajucu sa yśetkych stran tohto n-uholnika budeme nazyyaf kruźnicou w-uholni-ku ypisanou. Dokażeme, że plati poucka:

Veta 32. Do każdeho prayidelneho ?i-uholnika możno ypisaf krużnicu, która je siistredna s kruźnicou opisanou.

Aby sa hladana krużnica dotykała stran A_XA₂ a A₂A₃ (obr. 62), musi jej stred leżaf na osi uhla    aby sa dotykała stran

A₂A₃ a A₃A₄, musi jej stred leżaf na osi uhla <£ A₂A₃A₄ atd’.

Ak teda existuje krużnica ypisana do w-uholnika A_XA₂... A_n, pre-tinaju sa osi jeho ynutornych uhloy v jedinom bodę a obratene, ak sa pretinaju yśetky osi ynutornych uhlov w-uholnika A_XA₂— A_n v jedinom bodę, existuje krużnica ypisana do tohto w-uholnika.

Uvedena podmienka je pri pravidelnom n-uholniku splnena. Uhly <£ OA_xA₂ = OA₂A_x = OA₂A₃ = <£ OA_sA₂ = ... su totiż nayzajom zhodne, lebo trojuholniky A OA₁A₂, A OA₂A₃... A OA_nA_x

209