1954 Geometria 118

sdanymi stranami SA = a, AX = 6 (obr. 135). Vo vnutri useciek SA, AX zostrojme body A’, B tak, aby platilo

r*x'

Obr. 135

A’X’ = k.AX. Z toho vyplyva, ze X' s Y.

SA’ = l.SA = Xa, ~

AB = X.AX ~ X.b.

Trojuholnik AB A’ doplrlme na rovnobeżnik ABY A Dana rovnol’ahlos! preva-dza bod A do bodu Apriam-ku AX do priamky A’Y\\AX. Obraz X' bodu X leżi teda jednak na priamke A’Y, jednak na polpriamke SX, — t. j. v polrovine SAX, t. j. na polpriamke A’Y. Podia vety 1 plati pre dlżku usec-ky^'X'

AB — A’Y.

Pantograf je zostrojeny zo styroch latiek SA, AX, A'X', X'B, które su otacayo spojene v bodoch A, B, A', X' tak (obr. 136), aby vznikol

Obr. 136    '

rovnobeżnik ABX'A'. Ak upevnime bod S na podlożke a ak opisujeme bodom X (hrotom) napr. nejaku ciaru, opisuje bod X’ (ceruza) ciaru, ktorA je rovnoIahla podl’a stredu S, ako to znazorftuje obr, 135,

Tymto sposobom zostrojime k danemu utvaru utvar zmenscny v pomere A : 1. Keby sme opisovali dany utvar s bodom X', opisoval by bod Xutvar zv5<;seny v pomere 1 : A.

Pantografy su konśtruovane tak, że możno menif dlżky stran rovno-beżnika ABX’A’ a tym aj pomer zvacśenia alebo zmensenia. V praxi maju ramena SA, AŻ obyćajne rovnaku dlżku, t. j. a = b; potom je aj AB = A'X' — A AX = la — SA’.

Cvicenie

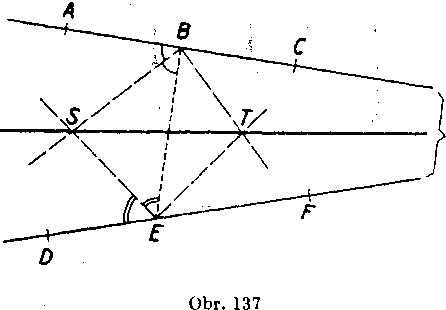
1. ABC, DEF su dve róznobeżky, które sa pretinaju mimo nakresne v bodę O (obr. 137). Oznaeime S priesecik os uhlov <t A BE,    BED,

T priesecik oś uhlor EBC, <£ BEF.

a)    Dokażte, że priamka ST obsahuje os uhla <£ BGE.

b)    Zostrojte tażnicu trojuholnika BGE prechadzajucu bodom G.

2.    Ćo vyplnia stredy useciek X Y, ak prebieha usećka X Y vśetkymi prie&kąmi A ABC, które su rovnobeżne so stranou AB¹. (Prieckou rozumieme usećku, która je urcena dvoma bodmi obvodu trojuholnika.)

3.    Urcte mnożinu bodov, których vzdialenosti od dvoch danych rózno-beżiek p, q su v pomere 2 : 3. Zvol’te róznobeżky p, q a narysujte.

4.    Je dany duty uhol <%AVB a bod M, który leżi yo ynutri uhki. Zostrojte useóku XY, której krajne body leżia na ramenach uhlbv; a która je bodom M rozdelena v pomere 3 : 1. Navod: Skumaj te obrazy polpriamok VA, VB v roynoJahloSti so stredom M a koefi-cięntoni — 3,